Chapter 9. Self-Organized Criticality
Sand Piles
In 1987, Bak, Tang, and Wiesenfeld published a paper in
Physical Review Letters, “Self-organized
criticality: An explanation of 
noise.” You can download it from
http://prl.aps.org/abstract/PRL/v59/i4/p381_1.
The title takes some explaining. A system is critical if it is in transition between two phases; for example, water at its freezing point is a critical system.
A variety of critical systems demonstrate common behaviors:
Long-tailed distributions of some physical quantities: for example, in freezing water, the distribution of crystal sizes is characterized by a power law.
Fractal geometries: freezing water tends to form fractal patterns—the canonical example is a snowflake. Fractals are characterized by self-similarity; that is, parts of the pattern resemble scaled copies of the whole.
Variations in time that exhibit pink noise: what we call “noise” is a time series with many frequency components. In white noise, all of the components have equal power. In pink noise, low-frequency components have more power than high-frequency components. Specifically, the power at frequency f is proportional to
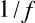. Visible light with this power
spectrum looks pink, hence the name.
Critical systems are usually unstable. For example, to keep water in a partially ...
Get Think Complexity now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
