Think Julia

Chapter 4. Case Study: Interface Design

This chapter presents a case study that demonstrates a process for designing functions that work together.

It introduces turtle graphics, a way to create programmatic drawings. Turtle graphics are not included in the standard library, so to use them you’ll have to add the ThinkJulia module to your Julia setup.

The examples in this chapter can be executed in a graphical notebook on JuliaBox, which combines code, formatted text, math, and multimedia in a single document (see Appendix B).

Turtles

A module is a file that contains a collection of related functions. Julia provides some modules in its standard library. Additional functionality can be added from a growing collection of packages.

Packages can be installed in the REPL by entering the Pkg REPL mode using the key ] and using the add command:

(v1.0) pkg> add https://github.com/BenLauwens/ThinkJulia.jl

This can take some time.

Before we can use the functions in a module, we have to import it with a using statement:

julia> using ThinkJulia

julia> 🐢 = Turtle()
Luxor.Turtle(0.0, 0.0, true, 0.0, (0.0, 0.0, 0.0))

The ThinkJulia module provides a function called Turtle that creates a Luxor.Turtle object, which we assign to a variable named 🐢(\:turtle: TAB).

Once you create a turtle, you can call a function to move it around. For example, to move the turtle forward:

@svg begin
    forward(🐢, 100)
end

The @svg keyword runs a macro that draws an SVG picture (Figure 4-1). Macros are an important but advanced feature of Julia.

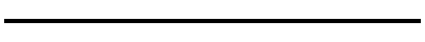
Figure 4-1. Moving the turtle forward

The arguments of forward are the turtle and a distance in pixels, so the actual size of the line that’s drawn depends on your display.

Each turtle is holding a pen, which is either down or up; if the pen is down (the default), the turtle leaves a trail when it moves. Figure 4-1 shows the trail left behind by the turtle. To move the turtle without drawing a line, first call the function penup. To start drawing again, call pendown.

Another function you can call with a turtle as an argument is turn for turning. The second argument for turn is an angle in degrees.

To draw a right angle, modify the macro call:

🐢 = Turtle()
@svg begin
    forward(🐢, 100)
    turn(🐢, -90)
    forward(🐢, 100)
end

Exercise 4-1

Now modify the macro to draw a square. Don’t go on until you’ve got it working!

Simple Repetition

Chances are you wrote something like this:

🐢 = Turtle()
@svg begin
    forward(🐢, 100)
    turn(🐢, -90)
    forward(🐢, 100)
    turn(🐢, -90)
    forward(🐢, 100)
    turn(🐢, -90)
    forward(🐢, 100)
end

We can do the same thing more concisely with a for statement:

julia> for i in 1:4
          println("Hello!")
       end
Hello!
Hello!
Hello!
Hello!

This is the simplest use of the for statement; we will see more later. But that should be enough to let you rewrite your square-drawing program. Don’t go on until you do.

Here is a for statement that draws a square:

🐢 = Turtle()
@svg begin
    for i in 1:4
        forward(🐢, 100)
        turn(🐢, -90)
    end
end

The syntax of a for statement is similar to a function definition. It has a header and a body that ends with the keyword end. The body can contain any number of statements.

A for statement is also called a loop because the flow of execution runs through the body and then loops back to the top. In this case, it runs the body four times.

This version is actually a little different from the previous square-drawing code because it makes another turn after drawing the last side of the square. The extra turn takes more time, but it simplifies the code if we do the same thing every time through the loop. This version also has the effect of leaving the turtle back in the starting position, facing in the starting direction.

Exercises

The following is a series of exercises using turtles. They are meant to be fun, but they have a point, too. While you are working on them, think about what the point is.

The following sections contain solutions to the exercises, so don’t look until you have finished (or at least tried them).

Exercise 4-2

Write a function called square that takes a parameter named t, which is a turtle. It should use the turtle to draw a square.

Exercise 4-3

Write a function call that passes 🐢 as an argument to square, and then run the macro again.

Exercise 4-4

Add another parameter, named len, to square. Modify the body so the length of the sides is len, and then modify the function call to provide a second argument. Run the macro again. Test with a range of values for len.

Exercise 4-5

Make a copy of square and change the name to polygon. Add another parameter named n and modify the body so it draws an $n$-sided regular polygon.

The exterior angles of an $n$-sided regular polygon are $\frac{360}{n}$ degrees.

Exercise 4-6

Write a function called circle that takes a turtle, t, and radius, r, as parameters and that draws an approximate circle by calling polygon with an appropriate length and number of sides. Test your function with a range of values of r.

Figure out the circumference of the circle and make sure that len * n == circumference.

Exercise 4-7

Make a more general version of circle called arc that takes an additional parameter angle, which determines what fraction of a circle to draw. angle is in units of degrees, so when angle = 360, arc should draw a complete circle.

Encapsulation

The first exercise asks you to put your square-drawing code into a function definition and then call the function, passing the turtle as a parameter. Here is a solution:

function square(t)
    for i in 1:4
        forward(t, 100)
        turn(t, -90)
    end
end
🐢 = Turtle()
@svg begin
    square(🐢)
end

The innermost statements, forward and turn, are indented twice to show that they are inside the for loop, which is inside the function definition.

Inside the function, t refers to the same turtle 🐢, so turn(t, -90) has the same effect as turn(🐢, -90). In that case, why not call the parameter 🐢? The idea is that t can be any turtle, not just 🐢 so you could create a second turtle and pass it as an argument to square:

🐫 = Turtle()
@svg begin
    square(🐫)
end

Wrapping a piece of code up in a function is called encapsulation. One of the benefits of encapsulation is that it attaches a name to the code, which serves as a kind of documentation. Another advantage is that if you reuse the code, it is more concise to call a function twice than to copy and paste the body!

Generalization

The next step is to add a len parameter to square. Here is a solution:

function square(t, len)
    for i in 1:4
        forward(t, len)
        turn(t, -90)
    end
end
🐢 = Turtle()
@svg begin
    square(🐢, 100)
end

Adding a parameter to a function is called generalization because it makes the function more general. In the previous version, the square is always the same size; in this version it can be any size.

The next step is also a generalization. Instead of drawing squares, polygon draws regular polygons with any number of sides. Here is a solution:

function polygon(t, n, len)
    angle = 360 / n
    for i in 1:n
        forward(t, len)
        turn(t, -angle)
    end
end
🐢 = Turtle()
@svg begin
    polygon(🐢, 7, 70)
end

This example draws a 7-sided polygon with side length 70.

Interface Design

The next step is to write circle, which takes a radius, r, as a parameter. Here is a simple solution that uses polygon to draw a 50-sided polygon:

function circle(t, r)
    circumference = 2 * π * r
    n = 50
    len = circumference / n
    polygon(t, n, len)
end

The first line computes the circumference of a circle with radius r using the formula 2πr. n is the number of line segments in our approximation of a circle, so len is the length of each segment. Thus, polygon draws a 50-sided polygon that approximates a circle with radius r.

One limitation of this solution is that n is a constant, which means that for very big circles, the line segments are too long, and for small circles, we waste time drawing very small segments. One solution would be to generalize the function by taking n as a parameter. This would give the user (whoever calls circle) more control, but the interface would be less clean.

The interface of a function is a summary of how it is used: What are the parameters? What does the function do? And what is the return value? An interface is “clean” if it allows the caller to do what he wants without dealing with unnecessary details.

In this example, r belongs in the interface because it specifies the circle to be drawn. n is less appropriate because it pertains to the details of how the circle should be rendered.

Rather than cluttering up the interface, it is better to choose an appropriate value of n depending on circumference:

function circle(t, r)
    circumference = 2 * π * r
    n = trunc(circumference / 3) + 3
    len = circumference / n
    polygon(t, n, len)
end

Now the number of segments is an integer near circumference/3, so the length of each segment is approximately 3, which is small enough that the circles look good but big enough to be efficient, and acceptable for any size circle.

Adding 3 to n guarantees that the polygon has at least three sides.

Refactoring

When I wrote circle, I was able to reuse polygon because a many-sided polygon is a good approximation of a circle. But arc is not as cooperative; we can’t use polygon or circle to draw an arc.

One alternative is to start with a copy of polygon and transform it into arc. The result might look like this:

function arc(t, r, angle)
    arc_len = 2 * π * r * angle / 360
    n = trunc(arc_len / 3) + 1
    step_len = arc_len / n
    step_angle = angle / n
    for i in 1:n
        forward(t, step_len)
        turn(t, -step_angle)
    end
end

The second half of this function looks like polygon, but we can’t reuse polygon without changing the interface. We could generalize polygon to take an angle as a third argument, but then polygon would no longer be an appropriate name! Instead, let’s call the more general function polyline:

function polyline(t, n, len, angle)
    for i in 1:n
        forward(t, len)
        turn(t, -angle)
    end
end

Now we can rewrite polygon and arc to use polyline:

function polygon(t, n, len)
    angle = 360 / n
    polyline(t, n, len, angle)
end

function arc(t, r, angle)
    arc_len = 2 * π * r * angle / 360
    n = trunc(arc_len / 3) + 1
    step_len = arc_len / n
    step_angle = angle / n
    polyline(t, n, step_len, step_angle)
end

Finally, we can rewrite circle to use arc:

function circle(t, r)
    arc(t, r, 360)
end

This process—rearranging a program to improve interfaces and facilitate code reuse—is called refactoring. In this case, we noticed that there was similar code in arc and polygon, so we “factored it out” into polyline.

If we had planned ahead, we might have written polyline first and avoided refactoring, but often you don’t know enough at the beginning of a project to design all the interfaces. Once you start coding, you understand the problem better. Sometimes refactoring is a sign that you have learned something.

A Development Plan

A development plan is a process for writing programs. The process we used in this case study is “encapsulation and generalization.” The steps of this process are:

1. Start by writing a small program with no function definitions.

2. Once you get the program working, identify a coherent piece of it, encapsulate the piece in a function, and give it a name.

3. Generalize the function by adding appropriate parameters.

4. Repeat steps 1–3 until you have a set of working functions. Copy and paste working code to avoid retyping (and redebugging).

5. Look for opportunities to improve the program by refactoring. For example, if you have similar code in several places, consider factoring it into an appropriately general function.

This process has some drawbacks—we will see alternatives later—but it can be useful if you don’t know ahead of time how to divide the program into functions. This approach lets you design as you go along.

Docstring

A docstring is a string before a function that explains the interface (“doc” is short for “documentation”). Here is an example:

"""
polyline(t, n, len, angle)

Draws n line segments with the given length and
angle (in degrees) between them.  t is a turtle.
"""
function polyline(t, n, len, angle)
    for i in 1:n
        forward(t, len)
        turn(t, -angle)
    end
end

Documentation can be accessed in the REPL or in a notebook by typing ? followed by the name of a function or macro, and pressing Enter:

help?> polyline
search:

  polyline(t, n, len, angle)

  Draws n line segments with the given length and angle (in degrees) between them. t is a turtle.

Docstrings are often triple-quoted strings, also known as “multiline” strings because the triple quotes allow the string to span more than one line.

A docstring contains the essential information someone would need to use the function. It explains concisely what the function does (without getting into the details of how it does it). It explains what effect each parameter has on the behavior of the function and what type each parameter should be (if it is not obvious).

Writing this kind of documentation is an important part of interface design. A well-designed interface should be simple to explain; if you have a hard time explaining one of your functions, maybe the interface could be improved.

Debugging

An interface is like a contract between a function and a caller. The caller agrees to provide certain parameters and the function agrees to do certain work.

For example, polyline requires four arguments: t has to be a turtle; n has to be an integer; len should be a positive number; and angle has to be a number, which is understood to be in degrees.

These requirements are called preconditions because they are supposed to be true before the function starts executing. Conversely, conditions at the end of the function are postconditions. Postconditions include the intended effect of the function (like drawing line segments) and any side effects (like moving the turtle or making other changes).

Preconditions are the responsibility of the caller. If the caller violates a (properly documented!) precondition and the function doesn’t work correctly, the bug is in the caller, not the function.

If the preconditions are satisfied and the postconditions are not, the bug is in the function. If your pre- and postconditions are clear, they can help with debugging.

Glossary

module

A file that contains a collection of related functions and other definitions.

package

An external library with additional functionality.

using statement

A statement that reads a module file and creates a module object.

loop

A part of a program that can run repeatedly.

encapsulation

The process of transforming a sequence of statements into a function definition.

generalization

The process of replacing something unnecessarily specific (like a number) with something appropriately general (like a variable or parameter).

interface

A description of how to use a function, including the name and descriptions of the arguments and return value.

refactoring

The process of modifying a working program to improve function interfaces and other qualities of the code.

development plan

A process for writing programs.

docstring

A string that appears at the top of a function definition to document the function’s interface.

precondition

A requirement that should be satisfied by the caller before a function starts.

postcondition

A requirement that should be satisfied by the function before it ends.

Exercises

Exercise 4-8

Enter the code in this chapter in a notebook.

1. Draw a stack diagram that shows the state of the program while executing circle(🐢, radius). You can do the arithmetic by hand or add print statements to the code.

2. The version of arc in “Refactoring” is not very accurate because the linear approximation of the circle is always outside the true circle. As a result, the turtle ends up a few pixels away from the correct destination. The solution shown here illustrates a way to reduce the effect of this error. Read the code and see if it makes sense to you. If you draw a diagram, you might see how it works.

   """
   arc(t, r, angle)
   
   Draws an arc with the given radius and angle:
   
       t: turtle
       r: radius
       angle: angle subtended by the arc, in degrees
   """
   function arc(t, r, angle)
       arc_len = 2 * π * r * abs(angle) / 360
       n = trunc(arc_len / 4) + 3
       step_len = arc_len / n
       step_angle = angle / n
   
       # making a slight left turn before starting reduces
       # the error caused by the linear approximation of the arc
       turn(t, -step_angle/2)
       polyline(t, n, step_len, step_angle)
       turn(t, step_angle/2)
   end

Exercise 4-9

Write an appropriately general set of functions that can draw flowers as in Figure 4-2.

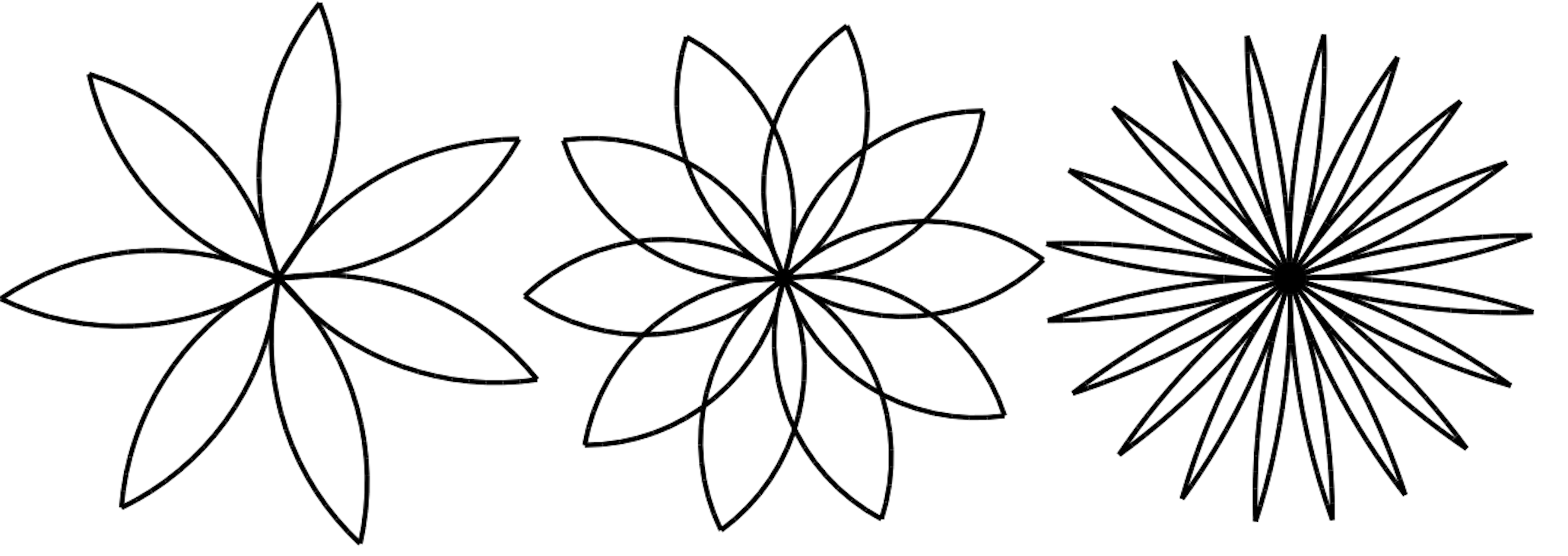
Figure 4-2. Turtle flowers

Exercise 4-10

Write an appropriately general set of functions that can draw shapes as in Figure 4-3.

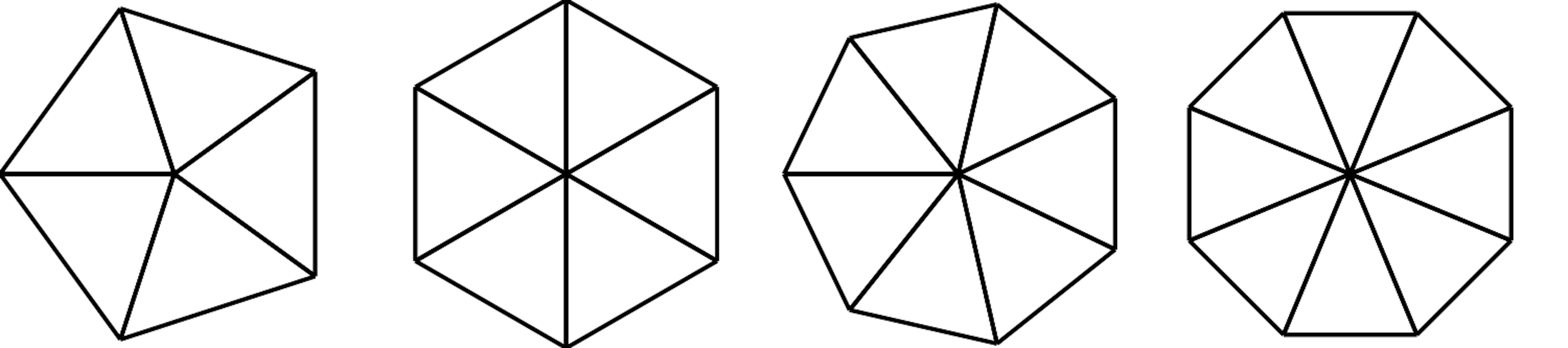
Figure 4-3. Turtle pies

Exercise 4-11

The letters of the alphabet can be constructed from a moderate number of basic elements, like vertical and horizontal lines and a few curves. Design an alphabet that can be drawn with a minimal number of basic elements and then write functions that draw the letters.

You should write one function for each letter, with names draw_a, draw_b, etc., and put your functions in a file named letters.jl.

Exercise 4-12

Read about spirals at https://en.wikipedia.org/wiki/Spiral; then write a program that draws an Archimedean spiral as in Figure 4-4.

Figure 4-4. Archimedean spiral