9.2. Fractal Geometry
In his essay "On Poetry—A Rhapsody" written in 1735, Jonathan Swift offers the following observation on the continuity of natural processes:
So, naturalists observe, a flea
Hath smaller fleas that on him prey;
And these have smaller still to bite 'em
And so proceed, ad infinitum.
Taking a large amount of anatomical license, one can illustrate this process by representing an idealized flea as an equilateral triangle, shown here under considerable magnification:
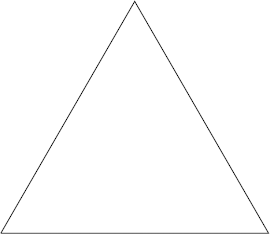
Putting a smaller flea on each of the two segments that form the back of the large flea illustrates the next stage in Swift's progression:
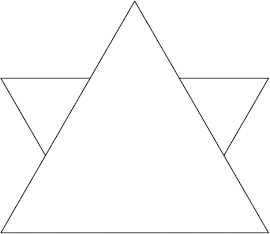
Each of these two new fleas can then play host to two smaller fleas, which leads to the following menagerie:

Clearly, this process can be repeated (as Swift suggests) ad infinitum with progressively tinier fleas.
Patterns such as this one have considerable mathematical significance and are known collectively as fractals. The term fractal was coined in 1975 by Benoit Mandelbrot, who synthesized several earlier mathematical discoveries to create a new geometry of fractal patterns. The principal defining characteristic of a fractal is that the components of a figure ...
Get Thinking Recursively with Java now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

