Thoughtful Machine Learning with Python

Chapter 4. Naive Bayesian Classification

Remember how email was several years ago? You probably recall your inbox being full of spam messages ranging from Nigerian princes wanting to pawn off money to pharmaceutical advertisements. It became such a major issue that we spent most of our time filtering spam.

Nowadays we spend a lot less time filtering spam than we used to, thanks to Gmail and tools like SpamAssassin. Using a method called a Naive Bayesian Classifier, such tools have been able to mitigate the influx of spam to our inboxes. This chapter will explore that topic as well as:

• Bayes’ theorem

• What a Naive Bayesian Classifier is and why it’s called “naive”

• How to build a spam filter using a Naive Bayesian Classifier

As noted in Table 2-2, a Naive Bayes Classifier is a supervised and probabilistic learning method. It does well with data in which the inputs are independent from one another. It also prefers problems where the probability of any attribute is greater than zero.

Using Bayes’ Theorem to Find Fraudulent Orders

Imagine you’re running an online store and lately you’ve been overrun with fraudulent orders. You estimate that about 10% of all orders coming in are fraudulent. In other words, in 10% of orders, people are stealing from you. Now of course you want to mitigate this by reducing the fraudulent orders, but you are facing a conundrum.

Every month you receive at least 1,000 orders, and if you were to check every single one, you’d spend more money fighting fraud than the fraud was costing you in the first place. Assuming that it takes up to 60 seconds per order to determine whether it’s fraudulent or not, and a customer service representative costs around $15 per hour to hire, that totals 200 hours and $3,000 per year.

Another way of approaching this problem would be to construct a probability that an order is over 50% fraudulent. In this case, we’d expect the number of orders we’d have to look at to be much lower. But this is where things become difficult, because the only thing we can determine is the probability that it’s fraudulent, which is 10%. Given that piece of information, we’d be back at square one looking at all orders because it’s more probable that an order is not fraudulent!

Let’s say that we notice that fraudulent orders often use gift cards and multiple promotional codes. Using this knowledge, how would we determine what is fraudulent or not—namely, how would we calculate the probability of fraud given that the purchaser used a gift card?

To answer for that, we first have to talk about conditional probabilities.

Conditional Probabilities

Most people understand what we mean by the probability of something happening. For instance, the probability of an order being fraudulent is 10%. That’s pretty straightforward. But what about the probability of an order being fraudulent given that it used a gift card? To handle that more complicated case, we need something called a conditional probability, which is defined as follows:

Equation 4-1. Conditional probability

$P\left(A\right|B)=\frac{P(A\cap B)}{P\left(B\right)}$

Probability Symbols

Generally speaking, writing P(E) means that you are looking at the probability of a given event. This event can be a lot of different things, including the event that A and B happened, the probability that A or B happened, or the probability of A given B happening in the past. Here we’ll cover how you’d notate each of these scenarios.

A ∩ B is called the intersection function but could also be thought of as the Boolean operation AND. For instance, in Python it looks like this:

a = [1,2,3]
b = [1,4,5]

set(a) & set(b) #=> [1]

A ∪ B could be called the OR function, as it is both A and B. For instance, in Python it looks like the following:

a = [1,2,3]
b = [1,4,5]

set(a) | set(b) #=> [1,2,3,4,5]

Finally, the probability of A given B looks as follows in Python:

a = set([1,2,3])
b = set([1,4,5])

total = 5.0

p_a_cap_b = len(a & b) / total
p_b = len(b) / total

p_a_given_b = p_a_cap_b / p_b #=> 0.33

This definition basically says that the probability of A happening given that B happened is the probability of A and B happening divided by the probability of B. Graphically, it looks something like Figure 4-1.

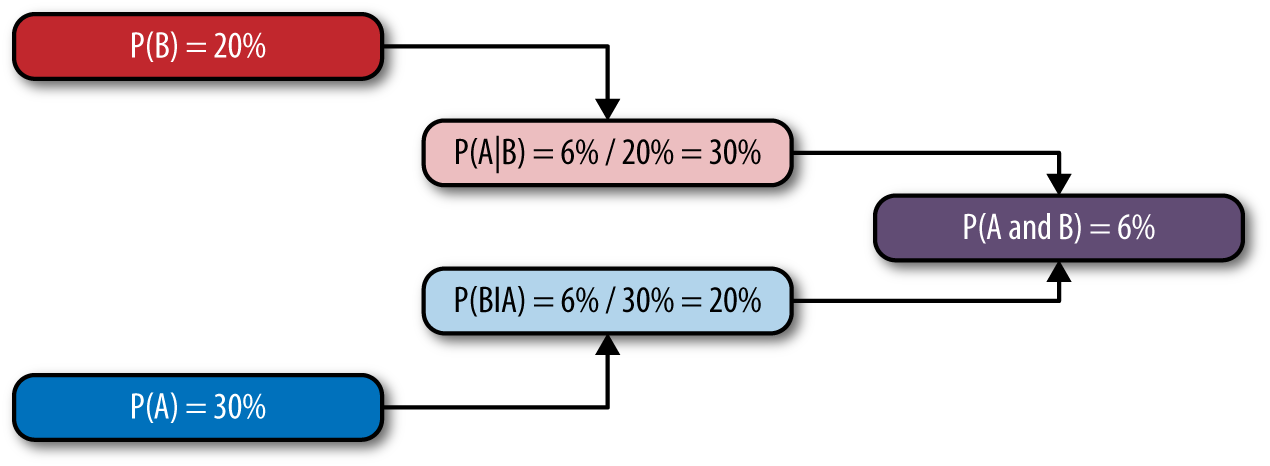
Figure 4-1. How conditional probabilities are made

This shows how P(A | B) sits between P(A and B) and P(B).

In our fraud example, let’s say we want to measure the probability of fraud given that an order used a gift card. This would be:

$P\left(Fraud\right|Giftcard)=\frac{P(Fraud\cap Giftcard)}{P\left(Giftcard\right)}$

Now this works if you know the actual probability of Fraud and Giftcard.

At this point, we are up against the problem that we cannot calculate P(Fraud|Giftcard) because that is hard to separate out. To solve this problem, we need to use a trick introduced by Bayes.

Inverse Conditional Probability (aka Bayes’ Theorem)

In the 1700s, Reverend Thomas Bayes came up with the original research that would become Bayes’ theorem. Pierre-Simon Laplace extended Bayes’ research to produce the beautiful result we know today. Bayes’ theorem is as follows:

Equation 4-2. Bayes’ theorem

$P(B\mid A)=\frac{P(A\mid B)P\left(B\right)}{P\left(A\right)}$

This is because of the following:

Equation 4-3. Bayes’ theorem expanded

$P(B\mid A)=\frac{\frac{P(A\cap B)P\left(B\right)}{P\left(B\right)}}{P\left(A\right)}=\frac{P(A\cap B)}{P\left(A\right)}$

This is useful in our fraud example because we can effectively back out our result using other information. Using Bayes’ theorem, we would now calculate:

$P(Fraud\mid Giftcard)=\frac{P(Giftcard\mid Fraud)P\left(Fraud\right)}{P\left(Giftcard\right)}$

Remember that the probability of fraud was 10%. Let’s say that the probability of gift card use is 10%, and based on our research the probability of gift card use in a fraudulent order is 60%. So what is the probability that an order is fraudulent given that it uses a gift card?

$P(Fraud\mid Giftcard)=\frac{60\%·10\%}{10\%}=60\%$

The beauty of this is that your work on measuring fraudulent orders is drastically reduced because all you have to look for is the orders with gift cards. Because the total number of orders is 1,000, and 100 of those are fraudulent, we will look at 60 of those fraudulent orders. Out of the remaining 900, 90 used gift cards, which brings the total we need to look at to 150!

At this point, you’ll notice we reduced the orders needing fraud review from 1,000 to 150 (i.e., 15% of the total). But can we do better? What about introducing something like people using multiple promo codes or other information?

Naive Bayesian Classifier

We’ve already solved the problem of finding fraudulent orders given that a gift card was used, but what about the problem of fraudulent orders given the fact that they have gift cards, or multiple promo codes, or other features? How would we go about that?

Namely, we want to solve the problem of $P(A\mid B,C)=?$. For this, we need a bit more information and something called the chain rule.

The Chain Rule

If you think back to probability class, you might recall that the probability of A and B happening is the probability of B given A times the probability of A. Mathematically, this looks like $P(A\cap B)=P\left(B\right|A\left)P\right(A)$. This is assuming these events are not mutually exclusive. Using something called a joint probability, this smaller result transforms into the chain rule.

Joint probabilities are the probability that all the events will happen. We denote this by using ∩. The generic case of the chain rule is:

Equation 4-4. Chain rule

$P(A_1,A_2,\cdots ,A_n)=P\left(A_1\right)P(A_2\mid A_1)P(A_3\mid A_1,A_2)\cdots P\left(A_n\right|A_1,A_2,\cdots ,A_{n-1})$

This expanded version is useful in trying to solve our problem by feeding lots of information into our Bayesian probability estimates. But there is one problem: this can quickly evolve into a complex calculation using information we don’t have, so we make one big assumption and act naive.

Naiveté in Bayesian Reasoning

The chain rule is useful for solving potentially inclusive problems, but we don’t have the ability to calculate all of those probabilities. For instance, if we were to introduce multiple promos into our fraud example, then we’d have the following to calculate:

$P(Fraud\mid Giftcard,Promos)=\frac{P(Giftcard,Promos\mid Fraud)P\left(Fraud\right)}{P(Giftcard,Promos)}$

Let’s ignore the denominator for now, as it doesn’t depend on whether the order is fraudulent or not. At this point, we need to focus on finding the calculation for P(Giftcard, Promos|Fraud)P(Fraud). If we apply the chain rule, this is equivalent to P(Fraud, Giftcard, Promos).

You can see this by the following (note that Fraud, Giftcard, and Promo have been abbreviated for space):

$P(F,G,P)=P\left(F\right)P(G,P|F)$

$P\left(F\right)P(G,P|F)=P(F\left)P\right(G\left|F\right)P\left(P\right|F,G)$

Now at this point we have a conundrum: how do you measure the probability of a promo code given fraud and gift cards? While this is the correct probability, it really can be difficult to measure—especially with more features coming in. What if we were to be a tad naive and assume that we can get away with independence and just say that we don’t care about the interaction between promo codes and gift cards, just the interaction of each independently with fraud?

In that case, our math would be much simpler:

$P(Fraud,Giftcard,Promo)=P\left(Fraud\right)P(Giftcard\mid Fraud)P(Promo\mid Fraud)$

This would be proportional to our numerator. And, to simplify things even more, we can assert that we’ll normalize later with some magical Z, which is the sum of all the probabilities of classes. So now our model becomes:

$P(Fraud\mid Giftcard,Promo)=\frac{1}{Z}P\left(Fraud\right)P(Giftcard\mid Fraud)P(Promo\mid Fraud)$

To turn this into a classification problem, we simply determine which input—fraud or not fraud—yields the highest probability. See Table 4-1.

Table 4-1. Probability of gift cards versus promos

	Fraud	Not fraud
Gift card present	60%	30%
Multiple promos used	50%	30%
Probability of class	10%	90%

At this point, you can use this information to determine whether an order is fraudulent based purely on whether it has a gift card present and whether it used multiple promos. The probability that an order is fraudulent given the use of gift cards and multiple promos is 62.5%. While we can’t exactly figure out how much savings this gives you in terms of the number of orders you must review, we know that we’re using better information and making a better judgment.

There is one problem, though: what happens when the probability of using multiple promos given a fraudulent order is zero? A zero result can happen for several reasons, including that there just isn’t enough of a sample size. The way we solve this is by using something called a pseudocount.

Pseudocount

There is one big challenge with a Naive Bayesian Classifier, and that is the introduction of new information. For instance, let’s say we have a bunch of emails that are classified as spam or ham. We build our probabilities using all of this data, but then something bad happens: a new spammy word, fuzzbolt. Nowhere in our data did we see the word fuzzbolt, and so when we calculate the probability of spam given the word fuzzbolt, we get a probability of zero. This can have a zeroing-out effect that will greatly skew results toward the data we have.

Because a Naive Bayesian Classifier relies on multiplying all of the independent probabilities together to come up with a classification, if any of those probabilities are zero then our probability will be zero.

Take, for instance, the email subject “Fuzzbolt: Prince of Nigeria.” Assuming we strip off of, we have the data shown in Table 4-2.

Table 4-2. Probability of word given ham or spam

Word	Spam	Ham
Fuzzbolt	0	0
Prince	75%	15%
Nigeria	85%	10%

Now let’s assume we want to calculate a score for ham or spam. In both cases, the score would end up being zero because fuzzbolt isn’t present. At that point, because we have a tie, we’d just go with the more common situation, which is ham. This means that we have failed and classified something incorrectly due to one word not being recognized.

There is an easy fix for that: pseudocount. When we go about calculating the probability, we add one to the count of the word. So, in other words, everything will end up being word_count + 1. This helps mitigate the zeroing-out effect for now. In the case of our fraud detector, we would add one to each count to ensure that it is never zero.

So in our preceding example, let’s say we have 3,000 words. We would give fuzzbolt a score of $\frac{1}{3000}$. The other scores would change slightly, but this avoids the zeroing-out problem.

Spam Filter

The canonical machine learning example is building a spam filter. In this section, we will work up a simple spam filter, SpamTrainer, using a Naive Bayesian Classifier and improve it by utilizing a 3-gram tokenization model.

As you have learned before, Naive Bayesian Classifiers can be easily calculated, and operate well under strongly independent conditions. In this example, we will cover the following:

• What the classes look like interacting with each other

• A good data source

• A tokenization model

• An objective to minimize our error

• A way to improve over time

Setup Notes

Python is constantly changing and I have tried to keep the examples working under both 3.5.x and 2.7.x Python. That being said, things might change as Python changes. For more comprehensive information check out the GitHub repo.

Coding and Testing Design

In our example, each email has an object that takes an .eml type text file that then tokenizes it into something the SpamTrainer can utilize for incoming email messages. See Figure 4-2 for the class diagram.

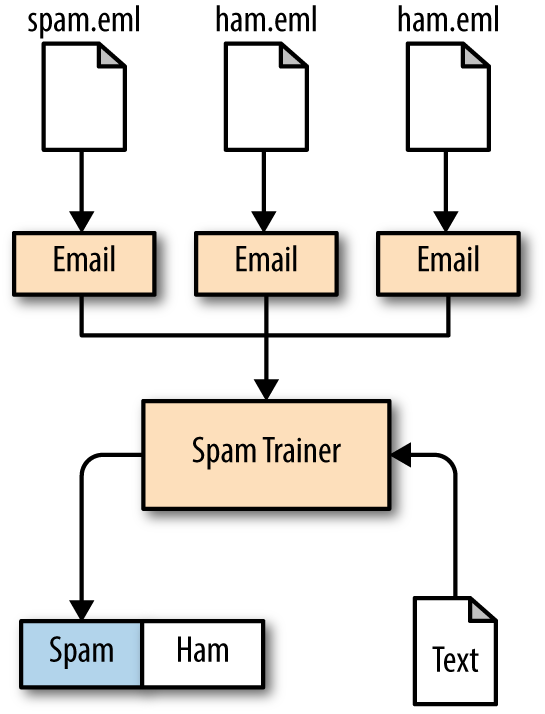
Figure 4-2. Class diagram showing how emails get turned into a SpamTrainer

When it comes to testing we will focus on the tradeoff between false positives and false negatives. With spam detection it becomes important to realize that a false positive (classifying an email as spam when it isn’t) could actually be very bad for business. We will focus on minimizing the false positive rate but similar results could be applied to minimizing false negatives or having them equal each other.

Data Source

There are numerous sources of data that we can use, but the best is raw email messages marked as either spam or ham. For our purposes, we can use the CSDMC2010 SPAM corpus.

This data set has 4,327 total messages, of which 2,949 are ham and 1,378 are spam. For our proof of concept, this should work well enough.

EmailObject

The EmailObject class has one responsibility, which is to parse an incoming email message according to the RFC for emails. To handle this, we use the standard library in Python because there’s a lot of nuance in there. In our model, all we’re concerned with is subject and body.

The cases we need to handle are HTML messages, plaintext, and multipart. Everything else we’ll just ignore. Building this class using test-driven development, let’s go through this step by step.

Starting with the simple plaintext case, we’ll copy one of the example training files from our data set under data/TRAINING/TRAIN_00001.eml to ./test/fixtures/plain.eml. This is a plaintext email and will work for our purposes. Note that the split between a message and header in an email is usually denoted by “\r\n\r\n”. Along with that header information is generally something like “Subject: A Subject goes here.” Using that, we can easily extract our test case, which is:

import unittest

import io
import re
from naive_bayes.email_object import EmailObject


class TestPlaintextEmailObject(unittest.TestCase):
  CLRF = "\n\n"

  def setUp(self):
    self.plain_file = './tests/fixtures/plain.eml'
    with io.open(self.plain_file, 'rb') as plaintext:
      self.text = plaintext.read().decode('utf-8')
      plaintext.seek(0)
      self.plain_email = EmailObject(plaintext)

  def test_parse_plain_body(self):
    body = self.CLRF.join(self.text.split(self.CLRF)[1:])
    self.assertEqual(self.plain_email.body(), body)

  def test_parses_the_subject(self):
    subject = re.search("Subject: (.*)", self.text).group(1)
    self.assertEqual(self.plain_email.subject(), subject)

Unit Testing in Python

Up until this point we haven’t introduced the unittest package in Python. Its main objective is to define unit tests for us to run on our code. Like similar unit testing frameworks in other languages like Ruby, we build a class that is prefixed with “Test” and then implement specific methods.

Methods to implement:

• Any method that is prefixed with test_ will be treated as a test to be run.

• setUp(self) is a special method that gets run before any test gets run. Think of this like a block of code that gets run before all tests (Table 4-3).

Table 4-3. Python unittest has many assertions we can use

Method	Checks
assertEqual(a, b)	a == b
assertNotEqual(a, b)	a != b
assertTrue(x)	bool(x) is True
assertFalse(x)	bool(x) is False
assertIs(a,b)	a is b
assertIsNot(a,b)	a is not b
assertIsNone(x)	x is None
assertIsNotNone(x)	x is not None
assertIn(a,b)	a in b
assertNotIn(a,b)	a not in b
assertIsInstance(a,b)	isinstance(a,b)
assertNotIsInstance(a,b)	not isinstance(a,b)

Do note that we will not use all of these methods; they are listed here for future reference.

Now instead of relying purely on regular expressions, we’ll use the standard library of Python. The standard library will handle all of the nitty-gritty details. Making email work for this particular case, we have:

import email
import sys

from bs4 import BeautifulSoup


class EmailObject(object):
  """
  Parses incoming email messages
  """
  CLRF = "\n\r\n\r"

  def __init__(self, infile, category=None):
    self.category = category
    if sys.version_info > (3, 0):
      # Python 3 code in this block
      self.mail = email.message_from_binary_file(infile)
    else:
      # Python 2 code in this block
      self.mail = email.message_from_file(infile)

  def subject(self):
    """
    Get message subject line
    :return: str
    """
    return self.mail.get('Subject')

  def body(self):
    """
    Get message body
    :return: str in Py3, unicode in Py2
    """
    payload = self.mail.get_payload()
    return self._single_body(self.mail)

  @staticmethod
  def _single_body(part):
    """
    Get text from part.
    :param part: email.Message
    :return: str body or empty str if body cannot be decoded
    """
    content_type = part.get_content_type()
    try:
      body = part.get_payload(decode=True)
    except Exception:
      return ''

    return body

Note

BeautifulSoup is a library that parses HTML and XML.

Now that we have captured the case of plaintext, we need to solve the case of HTML. For that, we want to capture only the inner_text. But first we need a test case, which looks something like this:

import unittest

import io
import re
from bs4 import BeautifulSoup
from naive_bayes.email_object import EmailObject

class TestHTMLEmail(unittest.TestCase):
  def setUp(self):
    with io.open('./tests/fixtures/html.eml', 'rb') as html_file:
      self.html = html_file.read().decode('utf-8')
      html_file.seek(0)
      self.html_email = EmailObject(html_file)

  def test_parses_stores_inner_text_html(self):
    body = "\n\n".join(self.html.split("\n\n")[1:])
    expected = BeautifulSoup(body, 'html.parser').text
    actual_body = self.html_email.body()
    self.assertEqual(actual_body, expected)

  def test_stores_subject(self):
    expected_subject = re.search("Subject: (.*)", self.html).group(1)
    actual_subject = self.html_email.subject()
    self.assertEqual(actual_subject, expected_subject)

As mentioned, we’re using BeautifulSoup to calculate the inner_text, and we’ll have to use it inside of the Email class as well. Now the problem is that we also need to detect the content_type. So we’ll add that in:

import email
import sys

from bs4 import BeautifulSoup


class EmailObject(object):

class EmailObject:
  # __init__
  # subject
  # body

  @staticmethod
  def _single_body(part):
    """
    Get text from part.
    :param part: email.Message
    :return: str body or empty str if body cannot be decoded
    """
    content_type = part.get_content_type()
    try:
      body = part.get_payload(decode=True)
    except Exception:
      return ''

    if content_type == 'text/html':
      return BeautifulSoup(body, 'html.parser').text
    elif content_type == 'text/plain':
      return body
    return ''

At this point, we could add multipart processing as well, but I will leave that as an exercise that you can try out yourself. In the coding repository mentioned earlier in the chapter, you can see the multipart version.

Now we have a working email parser, but we still have to deal with tokenization, or what to extract from the body and subject.

Tokenization and Context

As Figure 4-3 shows, there are numerous ways to tokenize text, such as by stems, word frequencies, and words. In the case of spam, we are up against a tough problem because things are more contextual. The phrase Buy now sounds spammy, whereas Buy and now do not. Because we are building a Naive Bayesian Classifier, we are assuming that each individual token is contributing to the spamminess of the email.

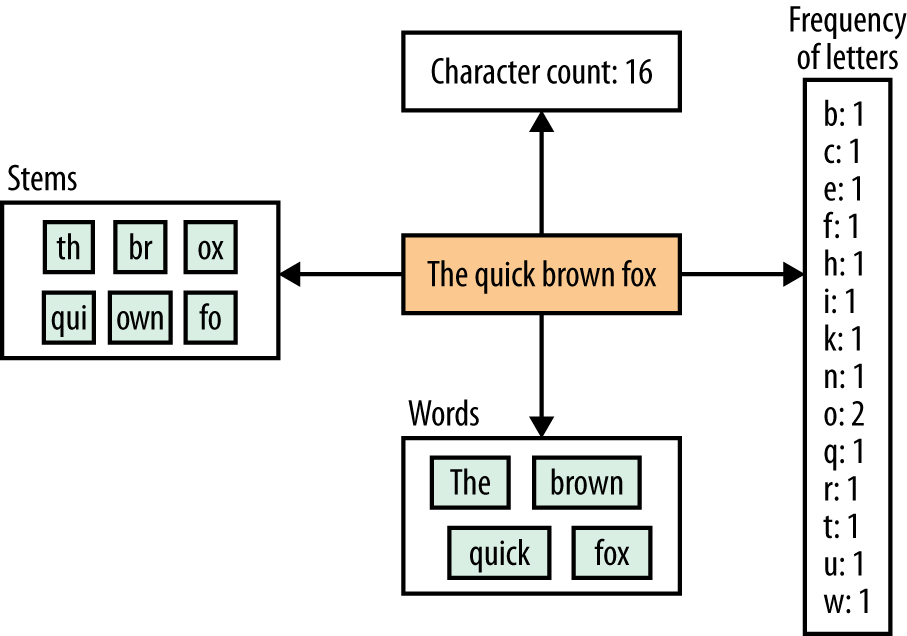
Figure 4-3. Lots of ways to tokenize text

The goal of the tokenizer we’ll build is to extract words into a stream. Instead of returning an array, we want to yield the token as it happens so that we are keeping a low memory profile. Our tokenizer should also downcase all strings to keep them similar:

import unittest

from naive_bayes.tokenizer import Tokenizer


class TestTokenizer(unittest.TestCase):
  def setUp(self):
    self.string = "this is a test of the emergency broadcasting system"

  def test_downcasing(self):
    expectation = ["this", "is", "all", "caps"]

    actual = Tokenizer.tokenize("THIS IS ALL CAPS")
    self.assertEqual(actual, expectation)

  def test_ngrams(self):
    expectation = [
      [u'\u0000', "quick"],
      ["quick", "brown"],
      ["brown", "fox"],
    ]

    actual = Tokenizer.ngram("quick brown fox", 2)
    self.assertEqual(actual, expectation)

As promised, we do two things in this tokenizer code. First, we lowercase all words. Second, instead of returning an array, we use a block. This is to mitigate memory constraints, as there is no need to build an array and return it. This makes it lazier. To make the subsequent tests work, though, we will have to fill in the skeleton for our tokenizer module like so:

class Tokenizer:
  """
  Splits lines by whitespaces, converts to lower case and builds n-grams.
  """
  NULL = u'\u0000'

  @staticmethod
  def tokenize(string):
    return re.findall("\w+", string.lower())

  @staticmethod
  def unique_tokenizer(string):
    return set(Tokenizer.tokenize(string))

  @staticmethod
  def ngram(string, ngram):
    tokens = Tokenizer.tokenize(string)

    ngrams = []

    for i in range(len(tokens)):
      shift = i - ngram + 1
      padding = max(-shift, 0)
      first_idx = max(shift, 0)
      last_idx = first_idx + ngram - padding

      ngrams.append(Tokenizer.pad(tokens[first_idx:last_idx], padding))

    return ngrams

  @staticmethod
  def pad(tokens, padding):
    padded_tokens = []

    for i in range(padding):
      padded_tokens.append(Tokenizer.NULL)

    return padded_tokens + tokens

Now that we have a way of parsing and tokenizing emails, we can move on to build the Bayesian portion: the SpamTrainer.

SpamTrainer

The SpamTrainer will accomplish three things:

• Storing training data

• Building a Bayesian classifier

• Error minimization through cross-validation

Storing training data

The first step we need to tackle is to store training data from a given set of email messages. In a production environment, you would pick something that has persistence. In our case, we will go with storing everything in one big dictionary.

Note

A set is a unique collection of data.

Remember that most machine learning algorithms have two steps: training and then computation. Our training step will consist of these substeps:

• Storing a set of all categories

• Storing unique word counts for each category

• Storing the totals for each category

So first we need to capture all of the category names; that test would look something like this:

import unittest

import io
from naive_bayes.email_object import EmailObject
from naive_bayes.spam_trainer import SpamTrainer


class TestSpamTrainer(unittest.TestCase):
  def setUp(self):
    self.training = [['spam', './tests/fixtures/plain.eml'],
                     ['ham', './tests/fixtures/small.eml'],
                     ['scram', './tests/fixtures/plain.eml']]
    self.trainer = SpamTrainer(self.training)
    with io.open('./tests/fixtures/plain.eml', 'rb') as eml_file:
      self.email = EmailObject(eml_file)

  def test_multiple_categories(self):
    categories = self.trainer.categories
    expected = set([k for k, v in self.training])
    self.assertEqual(categories, expected)

The solution is in the following code:

import io
from collections import defaultdict

from naive_bayes.tokenizer import Tokenizer
from naive_bayes.email_object import EmailObject


class SpamTrainer(object):
  """
  Storing training data
  Building a Bayesian classifier
  Error minimization through cross-validation
  """

  def __init__(self, training_files):
    self.categories = set()

    for category, _ in training_files:
      self.categories.add(category)

    self.totals = defaultdict(float)

    self.training = {c: defaultdict(float) for c in self.categories}

    self.to_train = training_files

  def total_for(self, category):
    """
    Get
    :param category:
    :return:
    """
    return self.totals[category]

You’ll notice we’re just using a set to capture this for now, as it’ll hold on to the unique version of what we need. Our next step is to capture the unique tokens for each email. We are using the special category called _all to capture the count for everything:

class TestSpamTrainer(unittest.TestCase):
  # setUp
  # test_multiple_categories

  def test_counts_all_at_zero(self):
    for cat in ['_all', 'spam', 'ham', 'scram']:
      self.assertEqual(self.trainer.total_for(cat), 0)

To get this to work, we have introduced a new method called train(), which will take the training data, iterate over it, and save it into an internal hash. The following is a solution:

class SpamTrainer(object):
  # __init__
  # total_for

  def train(self):
    for category, file in self.to_train:
      with io.open(file, 'rb') as eml_file:
        email = EmailObject(eml_file)

      self.categories.add(category)

      for token in Tokenizer.unique_tokenizer(email.body()):
        self.training[category][token] += 1
        self.totals['_all'] += 1
        self.totals[category] += 1

    self.to_train = {}

Now we have taken care of the training aspect of our program but really have no clue how well it performs. And it doesn’t classify anything. For that, we still need to build our classifier.

Building the Bayesian classifier

To refresh your memory, Bayes’ theorem is:

$P\left(A_i\right|B)=\frac{P(B\mid A_i)P\left(A_i\right)}{{\sum }_{j}P(B\mid A_j)P\left(A_j\right)}$

But because we’re being naive about this, we’ve distilled it into something much simpler:

Equation 4-5. Bayesian spam score

$Score(Spam,W_1,W_2,\cdots ,W_n)=P\left(Spam\right)P(W_1\mid Spam)P(W_2\mid Spam)\cdots P(W_n\mid Spam)$

which is then divided by some normalizing constant, Z.

Our goal now is to build the methods score, normalized_score, and classify. The score method will just be the raw score from the preceding calculation, while normalized_score will fit the range from 0 to 1 (we get this by dividing by the total sum, Z).

The score method’s test is as follows:

class TestSpamTrainer(unittest.TestCase):
  # setUp
  # test_multiple_categories
  # test_counts_all_at_zero

  def test_probability_being_1_over_n(self):
    trainer = self.trainer
    scores = list(trainer.score(self.email).values())

    self.assertAlmostEqual(scores[0], scores[-1])

    for i in range(len(scores) - 1):
      self.assertAlmostEqual(scores[i], scores[i + 1])

Because the training data is uniform across the categories, there is no reason for the score to differ across them. To make this work in our SpamTrainer object, we will have to fill in the pieces like so:

class SpamTrainer(object):
  # __init__
  # total_for
  # train

  def score(self, email):
    """
    Calculates score
    :param email: EmailObject
    :return: float number
    """
    self.train()

    cat_totals = self.totals

    aggregates = {cat: cat_totals[cat] / cat_totals['_all'] \
                  for cat in self.categories}

    for token in Tokenizer.unique_tokenizer(email.body()):
      for cat in self.categories:
        value = self.training[cat][token]
        r = (value + 1) / (cat_totals[cat] + 1)
        aggregates[cat] *= r

    return aggregates

This test does the following:

• First, it trains the model if it’s not already trained (the train method handles this).

• For each token of the blob of an email we iterate through all categories and calculate the probability of that token being within that category. This calculates the Naive Bayesian score of each without dividing by Z.

Now that we have score figured out, we need to build a normalized_score that adds up to 1. Testing for this, we have:

class TestSpamTrainer(unittest.TestCase):
  # setUp
  # test_multiple_categories
  # test_counts_all_at_zero
  # test_probability_being_1_over_n

  def test_adds_up_to_one(self):
    trainer = self.trainer
    scores = list(trainer.normalized_score(self.email).values())
    self.assertAlmostEqual(sum(scores), 1)
    self.assertAlmostEqual(scores[0], 1 / 2.0)

And subsequently on the SpamTrainer class we have:

class SpamTrainer(object):
  # __init__
  # total_for
  # train
  # score


  def normalized_score(self, email):
    """
    Calculates normalized score
    :param email: EmailObject
    :return: float number
    """
    score = self.score(email)
    scoresum = sum(score.values())

    normalized = {cat: (aggregate / scoresum) \
                  for cat, aggregate in score.items()}
    return normalized

Calculating a classification

Because we now have a score, we need to calculate a classification for the end user to use. This classification should take the form of an object that returns guess and score. There is an issue of tie breaking here.

Let’s say, for instance, we have a model that has turkey and tofu. What happens when the scores come back evenly split? Probably the best course of action is to go with which is more popular, whether it be turkey or tofu. What about the case where the probability is the same? In that case, we can just go with alphabetical order.

When testing for this, we need to introduce a preference order—that is, the occurrence of each category. A test for this would be:

class TestSpamTrainer(unittest.TestCase):
  # setUp
  # test_multiple_categories
  # test_counts_all_at_zero
  # test_probability_being_1_over_n
  # test_adds_up_to_one

  def test_preference_category(self):
    trainer = self.trainer
    expected = sorted(trainer.categories,
                      key=lambda cat: trainer.total_for(cat))

    self.assertEqual(trainer.preference(), expected)

Getting this to work is trivial and would look like this:

class SpamTrainer(object):
  # __init__
  # total_for
  # train
  # score
  # normalized_score

  def preference(self):
    return sorted(self.categories, key=lambda cat: self.total_for(cat))

Now that we have preference set up, we can test for our classification being correct. The code to do that is as follows:

class TestSpamTrainer(unittest.TestCase):
  # setUp
  # test_multiple_categories
  # test_counts_all_at_zero
  # test_probability_being_1_over_n
  # test_adds_up_to_one
  # test_preference_category

  def test_give_preference_to_whatever_has_the_most(self):
    trainer = self.trainer
    score = trainer.score(self.email)

    preference = trainer.preference()[-1]
    preference_score = score[preference]

    expected = SpamTrainer.Classification(preference, preference_score)
    self.assertEqual(trainer.classify(self.email), expected)

Getting this to work in code again is simple:

class SpamTrainer:
  # __init__
  # total_for
  # train
  # score
  # normalized_score
  # preference

  class Classification(object):
    """
    Guess and score
    """

    def __init__(self, guess, score):
      self.guess = guess
      self.score = score

    def __eq__(self, other):
      return self.guess == other.guess and self.score == other.score

  def classify(self, email):
    score = self.score(email)

    max_score = 0.0
    preference = self.preference()
    max_key = preference[-1]

    for k, v in score.items():
      if v > max_score:
        max_key = k
        max_score = v
      elif v == max_score and preference.index(k) > preference.index(max_key):
        max_key = k
        max_score = v
    return self.Classification(max_key, max_score)

Error Minimization Through Cross-Validation

At this point, we need to measure how well our model works. To do so, we need to take the data that we downloaded earlier and do a cross-validation test on it. From there, we need to measure only false positives, and then based on that determine whether we need to fine-tune our model more.

Minimizing false positives

Up until this point, our goal with making models has been to minimize error. This error could be easily denoted as the count of misclassifications divided by the total classifications. In most cases, this is exactly what we want, but in a spam filter this isn’t what we’re optimizing for. Instead, we want to minimize false positives. False positives, also known as Type I errors, are when the model incorrectly predicts a positive when it should have been negative.

In our case, if our model predicts spam when in fact the email isn’t, then the user will lose her emails. We want our spam filter to have as few false positives as possible. On the other hand, if our model incorrectly predicts something as ham when it isn’t, we don’t care as much.

Instead of minimizing the total misclassifications divided by total classifications, we want to minimize spam misclassifications divided by total classifications. We will also measure false negatives, but they are less important because we are trying to reduce spam that enters someone’s mailbox, not eliminate it.

To accomplish this, we first need to take some information from our data set, which we’ll cover next.

Building the two folds

Inside the spam email training data is a file called keyfile.label. It contains information about whether the file is spam or ham. Using that, we can build a cross-validation script. First let’s start with setup, which involves importing the packages we’ve worked on and some IO and regular expression libraries:

import io

from spam_trainer import SpamTrainer
from email_object import EmailObject

print("Cross Validation")

correct = 0
false_positives = 0.0
false_negatives = 0.0
confidence = 0.0

This doesn’t do much yet except start with a zeroed counter for correct, false positives, false negatives, and confidence. To set up the test we need to load the label data and turn that into a SpamTrainer object. We can do that using the following:

def label_to_training_data(fold_file):
  training_data = []

  for line in io.open(fold_file, 'r'):
    label_file = line.rstrip().split(' ')
    training_data.append(label_file)

  print(training_data)
  return SpamTrainer(training_data)

trainer = label_to_training_data('./tests/fixtures/fold1.label')

This instantiates a trainer object by calling the label_to_training_data function. Next we parse the emails we have in fold number 2:

def parse_emails(keyfile):
  emails = []
  print("Parsing emails for " + keyfile)

  for line in io.open(keyfile, 'r'):
    label, file = line.rstrip().split(' ')

    with io.open(file, 'rb') as eml_file:
      emails.append(EmailObject(eml_file, category=label))

  print("Done parsing files for " + keyfile)
  return emails

emails = parse_emails('./tests/fixtures/fold2.label')

Now we have a trainer object and emails parsed. All we need to do now is calculate the accuracy and validation metrics:

def validate(trainer, set_of_emails):
  correct = 0
  false_positives = 0.0
  false_negatives = 0.0
  confidence = 0.0

  for email in set_of_emails:
    classification = trainer.classify(email)
    confidence += classification.score

    if classification.guess == 'spam' and email.category == 'ham':
      false_positives += 1
    elif classification.guess == 'ham' and email.category == 'spam':
      false_negatives += 1
    else:
      correct += 1

  total = false_positives + false_negatives + correct

  false_positive_rate = false_positives / total
  false_negative_rate = false_negatives / total
  accuracy = (false_positives + false_negatives) / total
  message = """
  False Positives: {0}
  False Negatives: {1}
  Accuracy: {2}
  """.format(false_positive_rate, false_negative_rate, accuracy)
  print(message)


validate(trainer, emails)

Last, we can analyze the other direction of the cross-validation (i.e., validating fold1 against a fold2 trained model):

trainer = label_to_training_data('./tests/fixtures/fold2.label')
emails = parse_emails('./tests/fixtures/fold1.label')
validate(trainer, emails)

Cross-validation and error measuring

From here, we can actually build our cross-validation test, which will read fold1 and fold2 and then cross-validate to determine the actual error rate. The test looks something like this (see Table 4-4 for the results):

Cross Validation::Fold1 unigram model
  validates fold1 against fold2 with a unigram model

        False Positives: 0.0036985668053629217
        False Negatives: 0.16458622283865001
        Error Rate: 0.16828478964401294

Cross Validation::Fold2 unigram model
  validates fold2 against fold1 with a unigram model

        False Positives: 0.005545286506469501
        False Negatives: 0.17375231053604437
        Error Rate: 0.17929759704251386

Table 4-4. Spam versus ham

Category	Email count	Word count	Probability of email	Probability of word
Spam	1,378	231,472	31.8%	36.3%
Ham	2,949	406,984	68.2%	63.7%
Total	4,327	638,456	100%	100%

As you can see, ham is more probable, so we will default to that and more often than not we’ll classify something as ham when it might not be. The good thing here, though, is that we have reduced spam by 80% without sacrificing incoming messages.

Conclusion

In this chapter, we have delved into building and understanding a Naive Bayesian Classifier. As you have learned, this algorithm is well suited for data that can be asserted to be independent. Being a probablistic model, it works well for classifying data into multiple directions given the underlying score. This supervised learning method is useful for fraud detection, spam filtering, and any other problem that has these types of features.