book

Time Series Analysis: Forecasting and Control, Fourth Edition

Name: Time Series Analysis: Forecasting and Control, Fourth Edition
ISBN: 9780470272848

by George E. P. Box, Gregory C. Reinsel, Gwilym M. Jenkins

June 2008

Intermediate to advanced

770 pages

21h 9m

English

Wiley

Read now

Unlock full access

Cover Page
Title Page
Copyright
Dedication
Contents
Preface to the Fourth Edition
Preface to the Third Edition
CHAPTER ONE: Introduction
1.1 FIVE IMPORTANT PRACTICAL PROBLEMS1.2 STOCHASTIC AND DETERMINISTIC DYNAMIC MATHEMATICAL MODELS1.3 BASIC IDEAS IN MODEL BUILDING
PART ONE: Stochastic Models and Their Forecasting
CHAPTER TWO: Autocorrelation Function and Spectrum of Stationary Processes
2.1 AUTOCORRELATION PROPERTIES OF STATIONARY MODELS2.2 SPECTRAL PROPERTIES OF STATIONARY MODELSAPPENDIX A2.1 LINK BETWEEN THE SAMPLE SPECTRUM AND AUTOCOVARIANCE FUNCTION ESTIMATE

CHAPTER THREE: Linear Stationary Models
3.1 GENERAL LINEAR PROCESS3.2 AUTOREGRESSIVE PROCESSES3.3 MOVING AVERAGE PROCESSES3.4 MIXED AUTOREGRESSIVE–MOVING AVERAGE PROCESSESAPPENDIX A3.1 AUTOCOVARIANCES, AUTOCOVARIANCE GENERATING FUNCTION, AND STATIONARITY CONDITIONS FOR A GENERAL LINEAR PROCESSAPPENDIX A3.2 RECURSIVE METHOD FOR CALCULATING ESTIMATES OF AUTOREGRESSIVE PARAMETERS
CHAPTER FOUR: Linear Nonstationary Models
4.1 AUTOREGRESSIVE INTEGRATED MOVING AVERAGE PROCESSES4.2 THREE EXPLICIT FORMS FOR THE AUTOREGRESSIVE INTEGRATED MOVING AVERAGE MODEL4.3 INTEGRATED MOVING AVERAGE PROCESSESAPPENDIX A4.1 LINEAR DIFFERENCE EQUATIONSAPPENDIX A4.2 IMA(0, 1, 1) PROCESS WITH DETERMINISTIC DRIFTAPPENDIX A4.3 ARIMA PROCESSES WITH ADDED NOISE
CHAPTER FIVE: Forecasting
5.1 MINIMUM MEAN SQUARE ERROR FORECASTS AND THEIR PROPERTIES5.2 CALCULATING AND UPDATING FORECASTS5.3 FORECAST FUNCTION AND FORECAST WEIGHTS5.4 EXAMPLES OF FORECAST FUNCTIONS AND THEIR UPDATING5.5 USE OF STATE-SPACE MODEL FORMULATION FOR EXACT FORECASTING5.6 SUMMARYAPPENDIX A5.1 CORRELATIONS BETWEEN FORECAST ERRORSAPPENDIX A5.2 FORECAST WEIGHTS FOR ANY LEAD TIMEAPPENDIX A5.3 FORECASTING IN TERMS OF THE GENERAL INTEGRATED FORM
PART TWO: Stochastic Model Building
CHAPTER SIX: Model Identification
6.1 OBJECTIVES OF IDENTIFICATION6.2 IDENTIFICATION TECHNIQUES6.3 INITIAL ESTIMATES FOR THE PARAMETERS6.4 MODEL MULTIPLICITYAPPENDIX A6.1 EXPECTED BEHAVIOR OF THE ESTIMATED AUTOCORRELATION FUNCTION FOR A NONSTATIONARY PROCESSAPPENDIX A6.2 GENERAL METHOD FOR OBTAINING INITIAL ESTIMATES OF THE PARAMETERS OF A MIXED AUTOREGRESSIVE–MOVING AVERAGE PROCESS
CHAPTER SEVEN: Model Estimation
7.1 STUDY OF THE LIKELIHOOD AND SUM-OF-SQUARES FUNCTIONS7.2 NONLINEAR ESTIMATION7.3 SOME ESTIMATION RESULTS FOR SPECIFIC MODELS7.4 LIKELIHOOD FUNCTION BASED ON THE STATE-SPACE MODEL7.5 UNIT ROOTS IN ARIMA MODELS7.6 ESTIMATION USING BAYES'S THEOREMAPPENDIX A7.1 REVIEW OF NORMAL DISTRIBUTION THEORYAPPENDIX A7.2 REVIEW OF LINEAR LEAST SQUARES THEORYAPPENDIX A7.3 EXACT LIKELIHOOD FUNCTION FOR MOVING AVERAGE AND MIXED PROCESSESAPPENDIX A7.4 EXACT LIKELIHOOD FUNCTION FOR AN AUTOREGRESSIVE PROCESSAPPENDIX A7.5 ASYMPTOTIC DISTRIBUTION OF ESTIMATORS FOR AUTOREGRESSIVE MODELSAPPENDIX A7.6 EXAMPLES OF THE EFFECT OF PARAMETER ESTIMATION ERRORS ON VARIANCES OF FORECAST ERRORS AND PROBABILITY LIMITS FOR FORECASTSAPPENDIX A7.7 SPECIAL NOTE ON ESTIMATION OF MOVING AVERAGE PARAMETERS
CHAPTER EIGHT: Model Diagnostic Checking
8.1 CHECKING THE STOCHASTIC MODEL8.2 DIAGNOSTIC CHECKS APPLIED TO RESIDUALS8.3 USE OF RESIDUALS TO MODIFY THE MODEL
CHAPTER NINE: Seasonal Models
9.1 PARSIMONIOUS MODELS FOR SEASONAL TIME SERIES9.2 REPRESENTATION OF THE AIRLINE DATA BY A MULTIPLICATIVE (0, 1, 1) × (0, 1, 1) 12 MODEL9.3 SOME ASPECTS OF MORE GENERAL SEASONAL ARIMA MODELS9.4 STRUCTURAL COMPONENT MODELS AND DETERMINISTIC SEASONAL COMPONENTS9.5 REGRESSION MODELS WITH TIME SERIES ERROR TERMSAPPENDIX A9.1 AUTOCOVARIANCES FOR SOME SEASONAL MODELS
CHAPTER TEN: Nonlinear and Long Memory Models
10.1 AUTOREGRESSIVE CONDITIONAL HETEROSCEDASTIC (ARCH) MODELS10.2 NONLINEAR TIME SERIES MODELS10.3 LONG MEMORY TIME SERIES PROCESSES
PART THREE: Transfer Function and Multivariate Model Building
CHAPTER ELEVEN: Transfer Function Models
11.1 LINEAR TRANSFER FUNCTION MODELS11.2 DISCRETE DYNAMIC MODELS REPRESENTED BY DIFFERENCE EQUATIONS11.3 RELATION BETWEEN DISCRETE AND CONTINUOUS MODELSAPPENDIX A11.1 CONTINUOUS MODELS WITH PULSED INPUTSAPPENDIX A11.2 NONLINEAR TRANSFER FUNCTIONS AND LINEARIZATION
CHAPTER TWELVE: Identification, Fitting, and Checking of Transfer Function Models
12.1 CROSS-CORRELATION FUNCTION12.2 IDENTIFICATION OF TRANSFER FUNCTION MODELS12.3 FITTING AND CHECKING TRANSFER FUNCTION MODELS12.4 SOME EXAMPLES OF FITTING AND CHECKING TRANSFER FUNCTION MODELS12.5 FORECASTING WITH TRANSFER FUNCTION MODELS USING LEADING INDICATORS12.6 SOME ASPECTS OF THE DESIGN OF EXPERIMENTS TO ESTIMATE TRANSFER FUNCTIONSAPPENDIX A12.1 USE OF CROSS SPECTRAL ANALYSIS FOR TRANSFER FUNCTION MODEL IDENTIFICATIONAPPENDIX A12.2 CHOICE OF INPUT TO PROVIDE OPTIMAL PARAMETER ESTIMATES
CHAPTER THIRTEEN: Intervention Analysis Models and Outlier Detection
13.1 INTERVENTION ANALYSIS METHODS13.2 OUTLIER ANALYSIS FOR TIME SERIES13.3 ESTIMATION FOR ARMA MODELS WITH MISSING VALUES
CHAPTER FOURTEEN: Multivariate Time Series Analysis
14.1 STATIONARY MULTIVARIATE TIME SERIES14.2 LINEAR MODEL REPRESENTATIONS FOR STATIONARY MULTIVARIATE PROCESSES14.3 NONSTATIONARY VECTOR AUTOREGRESSIVE-MOVING AVERAGE MODELS14.4 FORECASTING FOR VECTOR AUTOREGRESSIVE-MOVING AVERAGE PROCESSES14.5 STATE-SPACE FORM OF THE VECTOR ARMA MODEL14.6 STATISTICAL ANALYSIS OF VECTOR ARMA MODELS14.7 EXAMPLE OF VECTOR ARMA MODELING
PART FOUR: Design of Discrete Control Schemes
CHAPTER FIFTEEN: Aspects of Process Control
15.1 PROCESS MONITORING AND PROCESS ADJUSTMENT15.2 PROCESS ADJUSTMENT USING FEEDBACK CONTROL15.3 EXCESSIVE ADJUSTMENT SOMETIMES REQUIRED BY MMSE CONTROL15.4 MINIMUM COST CONTROL WITH FIXED COSTS OF ADJUSTMENT AND MONITORING15.5 FEEDFORWARD CONTROL15.6 MONITORING VALUES OF PARAMETERS OF FORECASTING AND FEEDBACK ADJUSTMENT SCHEMESAPPENDIX A15.1 FEEDBACK CONTROL SCHEMES WHERE THE ADJUSTMENT VARIANCE IS RESTRICTEDAPPENDIX A15.2 CHOICE OF THE SAMPLING INTERVAL
PART FIVE: Charts and Tables
Collection of Tables and Charts
Collection of Time Series Used for Examples in the Text and in Exercises
References
PART SIX: Exercises and Problems
CHAPTER 2CHAPTER 3CHAPTER 4CHAPTER 5CHAPTER 6CHAPTER 7CHAPTER 8CHAPTER 9CHAPTER 10CHAPTER 11CHAPTER 12CHAPTER 13CHAPTER 14CHAPTER 15
Index

Content preview from Time Series Analysis: Forecasting and Control, Fourth Edition

CHAPTER THREE

Linear Stationary Models

A general linear stochastic model is described that supposes a time series to be generated by a linear aggregation of random shocks. For practical representation it is desirable to employ models that use parameters parsimoniously. Parsimony may often be achieved by representation of the linear process in terms of a small number of autoregressive and moving average terms. The properties of the resulting autoregressive–moving average (ARMA) models are discussed in preparation for their use in model building.

3.1 GENERAL LINEAR PROCESS

3.1.1 Two Equivalent Forms for the Linear Process

In Section 1.2.1 we discussed the representation of a stochastic process as the output from a linear filter, whose input is white noise a_t, that is,

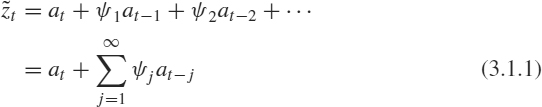
where is the deviation of the process from some origin, or from its mean, if the process is stationary. The general linear process (3.1.1) allows us to represent as a weighted sum of present and past values of the “white noise” process a_t. The literature provides many important references on the development of linear stochastic models [32, 106, 130, 135, 136, 178, 239, 240, 251, 265, 298, 311, 317]. The white noise process ...

Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
and much more.

Read now

Unlock full access

More than 5,000 organizations count on O’Reilly

O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.

Julian F.

Head of Cybersecurity

I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.

Addison B.

Field Engineer

I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.

Amir M.

Data Platform Tech Lead

I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.

Mark W.

Embedded Software Engineer

Analysis of Financial Time Series, Third Edition

Publisher Resources

ISBN: 9780470272848Purchase book

Cloud Computing

Data Engineering

Data Science

AI & ML

Programming Languages

Software Architecture

IT/Ops

Security

Design

Business