Transformer Engineering, 2nd Edition

$V^e={\displaystyle \sum _{j=1}^2{N}_j^e{V}_j^e}.$

(12.94)

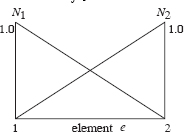
Figure 12.10 1-D Shape functions.

$N_j^e$ denotes the interpolation or shape functions which are given by

$N_1^e=\frac{r_2^e-r}{l^e}\mathrm{and}{N}_2^e=\frac{r-r_1^e}{l^e}$

(12.95)

where $l^e=r_2^e-r_1^e.$ The functions $N_j^e,$ which depend on the independent variable r, are shown in Figure 12.10. $N_1^e(N_2^e)$ equals 1 at node 1 (2) and zero at node 2 (1); at any intermediate point its value is a fraction between 0 and 1. This is an obvious result given the expression, as in Equation 12.94, for voltage at any point within the element, $V^e=N_1^e{\nabla }_1^e+N_2^e{\nabla }_2^e.$ For example, at node 1, $V^e=V_1^e$ leading to $N_1^e=1$ and $N_2^e=0$. Thus, for the nodes, ${\left(N_i^e\right)}_j={\delta }_{ij},$ where δ_ij = 1 ...