Understanding and Applying Basic Statistical Methods Using R

Chapter 7HYPOTHESIS TESTING

The previous chapter described confidence intervals, which provide a fundamental strategy for making inferences about population measures of location such as the population mean and the population median. About a century after Laplace's groundbreaking work on sampling distributions, new techniques were developed for making inferences about parameters that add perspective and are routinely used. One of the main architects of this new perspective was Jerzy Neyman. Forced to leave Poland due to the war between Poland and Russia, Neyman eventually moved to London in 1924 where he met Egon Pearson (son of Karl Pearson, whom we met in Chapter 1). Their joint efforts led to the Neyman–Pearson framework for testing hypotheses, which is the subject of this chapter.

7.1 Testing Hypotheses about the Mea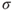n, Known

The essence of hypothesis testing methods is quite simple. A researcher formulates some speculation about the population under study. Typically, the speculation has to do with the value of some unknown population parameter, such as the population mean. Then, data are analyzed with the goal of determining whether the stated speculation is unreasonable. That is, is there empirical evidence indicating that the speculation is probably incorrect? The speculation ...