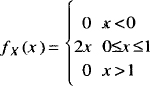Typesetting Equations with eqn
Typesetting mathematical equations has always been a problem for users who have a limited knowledge of mathematics or typesetting. This is because mathematical expressions are often a mixture of standard text and special characters in different point sizes. For example, the equation:
![]()
requires three special charactrs (Σ, ∞, and →)and roman and italic characters in two different sizes. Expressions also may require horizontal and vertical printing motions (as in subscripts and superscripts).
You could code this example using troff requests, but the syntax for describing the printing motions, sizes, and fonts are difficult to learn and difficult to type in correctly. UNIX has formatting tools specifically designed for documents containing mathematical symbols—the programs eqn and neqn. The eqn program is a preprocessor for troff; neqn is a preprocessor for nroff.
With eqn you can typeset both inline equations and equations that are set off from the body of the text like the example shown. It takes an English-like description of a mathematical equation and generates a troff script. You don’t need to understand what you are typing.
The eqn preprocessor was designed to be easy to learn and even easier to use. This implies that normal mathematical conventions such as operator precedence and parentheses cannot be used. Nor does eqn assume that parentheses are always balanced, or that an expression is better written in another form. There are only a few rules, keywords, special symbols, and operators to remember. If something works in one situation, it should work everywhere.
This section shows you how to typeset mathematical equations using a set of special words that belong to the eqn vocabulary. With eqn, you can format the following quite easily:
![]() special symbols, such as summations (Σ), products (Π) integrals (∫), and square roots
special symbols, such as summations (Σ), products (Π) integrals (∫), and square roots ![]()
![]() positional notation, such as subscripts and superscripts, fractions, matrices, and vertical piles
positional notation, such as subscripts and superscripts, fractions, matrices, and vertical piles
![]() diacritical marks
diacritical marks
![]() sizes and fonts
sizes and fonts
![]() horizontal and vertical spacing
horizontal and vertical spacing
You can even define a string that appears repeatedly throughout the document so that you do not need to type it in each time it appears.
▪ A Simple eqn Example ▪
To best illustrate how eqn works and how easy it is to learn the syntax, let’s take a simple example:
![]()
If you were to read this mathematical expression aloud to another person, you might say “a sub 2 over b.” This is exactly how you would describe the expression to eqn. The word sub denotes a subscript; the word over denotes a fraction. You will see the other words that eqn treats as special (i.e., that belong to the eqn vocabulary) as we move along in this section.
When you use eqn, it assumes that you have a two-dimensional picture of how the equation should appear in the document. The key in writing the eqn decription is to familiarize yourself with the special words used by eqn in printing mathematical characters. Then, describe the equation as if you were reading it aloud to another person.
The eqn preprocessor takes care of the standard things that you would expect to happen automatically, such as printing superscripts and subscripts in an appropriately smaller size, and adjusting the length and size of fraction bars. Following mathematical convention, variables are made italic, parentheses, operators, and digits are made roman, and normal spacing is automatically adjusted to make the expression look better.
▪ Using eqn ▪
The eqn preprocessor is used not only for typesetting equations, but also for typesetting nontechnical documents. For example, many documents contain subscripted or superscripted words. Using eqn can be easier than formatting the subscript or superscript using troff commands.
To format a document with eqn, you would enter:
$ eqn /usr/pub/eqnchar files | troff [options]
You can then pipe the output to the desired printer. The file /usr/pub/eqnchar contains definitions of additional special characters that can be used by eqn. It is not essential that you use it, but you may get better results with certain equations if you do.
If you use eqn with the tbl preprocessor to print tables containing mathematical expressions, invoke tbl before eqn to mimimize the data passed through the pipe:
$ tbl /usr/pub/eqnchar file | eqn | troff
If you are using nroff instead of troff, you can get a reasonable approximation of eqn output by using neqn. However, printers used with nroff may be unable to print many of the special characters used in equations.
▪ Specifying Equations ▪
Mathematical documents contain both displayed equations and standard text mixed with mathematical expressions. The eqn preprocessor allows you to typeset both forms.
Displayed Equations
For equations that appear outside the body of the text, mark the beginning of each equation with an .EQ and the end with an .EN. Note that these delimiters may or may not also be defined as macros. They are recognized by eqn as flags to begin and end processing.
If they are not defined as macros by the package you are using, you can define them yourself, or can simply supplement them with troff requests (such as .ce to center the equation) as desired.
If you are using the ms macro package, .EQ and .EN are defined as macros, and the equation is centered by default. Thus, if you type:
.EQ
C=Ax+By
.EN
the output will be:
C =Ax+By
In ms, you can also left justify the equation using .EQ L or indent it using .EQ I. You can further specify an arbitrary equation number or label that will be printed at the right margin. For example, the lines:
.EQ I (13a)
C=Ax+By
.EN
![]()
The mathematical symbols +, −, =, and ( ) are typed in just as they appear in the equation.
If you’re using the mm macro package, put the .EQ/ .EN pair inside a. DS/. DE pair so that the format looks like this:
.DS
.EQ
equation
.EN
.DE
This automatically centers the displayed equation. You can also use a break producing request (such as .br or . sp) immediately following the .DS macro but before the .EQ macro to display the equation at the left margin of the text.
Inline Expressions
If you are using ms or mm, .EQ and .EN imply a displayed equation and so cannot be used for short inline expressions. But eqn provides a shorthand notation for displaying this type of expression. You can define any two characters as delimiters to mark the beginning and end of an inline equation, and then type the expression right in the middle of the text. To do this, define the equation delimiters within an .EQ and an .EN at the beginning of your file.
For example, to set both delimiters to #, add the following lines:
.EQ
delim ##
.EN
If you’re using mm, do not use the .DS/. DE pair to enclose a .EQ/ .EN pair that only defines the delimiters for inline equations. If you do, extra blank lines will appear in the output.
Do not use braces ({ }), a circumflex (^), a tilde (~), or double quotation marks (”) as delimiters because these have a special meaning to eqn. Choose characters that you are unlikely to use within any equation in the document. After you have defined your delimiter, you can begin using it within a line of text as in the following example:
The possible prices of an ice cream cone in cents are
#y sub 1 = 75 #, #y sub 2 = 85 #, and #y sub 3 = 95#.
This produces the line:
Assume that the possible prices of an ice cream cone in cents are y1=76, y2=85, and y3=95.
The eqn program leaves enough room before and after a line containing inline expressions with fractions or large characters so that they don’t interfere with the surrounding lines.
To turn off the delimiters, use:
.EQ
delim off
.EN
Throughout this section, we will use the delimiters ## in our eqn examples. However, we will typically show the results as a displayed equation.
▪ Spaces in Equations ▪
You may have noticed in the previous example that the word sub is surrounded by blanks, and the subscript is separated from the = sign with a blank. Spaces and new lines are used to tell eqn that certain words belong to the eqn vocabulary and deserve special treatment. The spaces and new lines that you type in the input equation do not appear in the printed output.
For example, all of the following equations:
#C=Ax+By#
#C = Ax + By#
#C= A x +
BY #
produce the same output:
C =Ax +By
Note that the spaces and newlines were ignored by eqn.
You should use spaces as freely as possible to break up more complex equations and make your input more readable and easier to edit. Remember that any spaces or newlines you enter within an equation are not printed out. This is often a point of confusion for new users. If your equation doesn’t turn out the way it should, chances are you missed typing in a space somewhere. A useful rule of thumb is: when in doubt, use a space.
Printing Spaces in the Output
You may want to fine-tune the printed appearance of an equation by adding spaces between groups of terms. If you want to print spaces in the output, use a tilde (~) for each space. A circumflex (^) gives a space half the width of a tilde. For example:
#C~=~Ax~+~By#
yields:
c = Ax + By
and:
#C^=^Ax^+^By#
yields:
C =Ax + By
You can also use tabs to separate parts of an equation, but the tab stops must set by the troff .ta request. For example:
.ta li 1.5i 2i 2.5i
. EQ
x sub 1
+x sub 2
+ s sub 1
=10
.EN
.EQ
−2 x sub 1
+s sub 1
=42
.EN
yields:
![]()
(Note that each equation must have its own pair of .EQ/ .EN delimiters.) Another way of aligning equations uses the eqn words mark and lineup, as you will see later.
Subscripts and Superscripts: A Common Use
Perhaps the most common application of eqn is in generating subscripts and superscripts within a line of text or a table. As you have seen in previous examples, subscripts are denoted by the word sub. Superscripts are designated by sup. For example:
#y sub 1 = x sup 2^+^1#
yields:
y1,=x2+ 1
There are two simple rules to remember in writing subscripts and superscripts:
1. Put at least one space or space delimiter (such as ^ or ~) befor and after the words sup and sub.
2. Leave at least one space or space delimiter after the subscript or superscript.
Let’s see the effect on the output when you omit necessary spaces. For example:
#y sub 1 =x sup2^+^1#
yields:
y1=x sup 2+ 1
#y sub 1 =x sup 2+^1#
yields:
![]()
If you don’t leave a space after sub or sup (as in the first example), eqn will not recognize them as special words, and so will not produce a subscript or superscript. Also, if you don’t leave a space after the subscript or superscript, eqn thinks that the character(s) following it are still part of the subscript or superscript. This is a very common mistake made by new users.
You can also write subscripted subscripts and superscripted superscripts. If a superscript and subscript both appear for the same item, sub should come before sup. Therefore:
#a sub k sup 2 #
yields:
![]()
Reversing the order of the words:
#a sup 2 sub k#
yields:
![]()
Some equations also require you to type chemical symbols like:
2He4
Because sup technically means a superscript on something, you must use a placeholder (a pair of double quotation marks) before the word sup and write this expression as:
#"" sup 2 He sub 4 #
▪ Using Braces for Grouping ▪
Normally, you would use a blank or a space delimiter to signal the end of a subscript or superscript. But if your subscript or superscript consists of two or more characters or words separated by blanks, or if you are writing nested subscripts or superscripts, this will not work. In this case, use braces to mark the beginning and end of your subscript or superscript.
#r sub {i=5;t=10^years]#
yields:
ri=5;t=lOyears
In contrast, this line without the braces:
#r sub i=5;t=10^years#
yields:
ri=5;t=10years
In the first example, we used braces to force eqn to treat the string:
i=5;t=10 years
as a subscript. Use braces to make your intent perfectly clear whenever you are unsure of how eqn will treat the equation. You can also use braces within braces, as in the line:
#e sup { i sup {k+l}]#
which yields:
eik + l
Make sure that a left brace always has a corresponding right brace.
If you have to print braces in your document, enclose them in double quotation marks like “ { “ and ” ) ”.
▪ Special Character Names ▪
In many mathematical equations, you use the Greek alphabet to define variables. To print Greek letters, spell them out in the case that you want. For example, delta produces δ, and DELTA gives Δ. Thus, you only need to spell out the character π, as in:
#pi r sup 2#
to print:
πr2
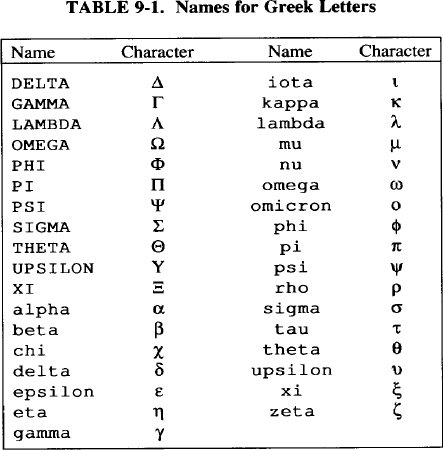
Note that special names don’t exist for all uppercase Greek letters, such as ALPHA or ETA, because they are identical to the equivalent English letters. See Table 9-1 for a list of Greek letters.
A common mistake is to forget to put a space around the Greek name. For example, typing:
#f (theta)#
yields:
f (theta)
and not:
f (θ)
which is what we want. Because there are no spaces surrounding the word theta, eqn doesn’t recognize it as a special word.
You can also use troff four-character names for characters, as in the description:
#c = a \(pl b#
which yields:
C = a+b
▪ Special Symbols ▪
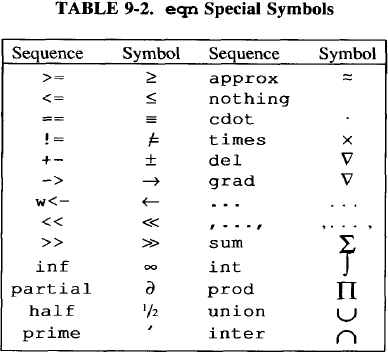
The eqn program recognizes the sequences in Table 9-2 as belonging to the eqn vocabulary, and translates them to the appropriate symbols.
The following examples illustrate the use of these character sequences.
#C sub 0 prime
yields:
Co’
and:
# O <= a <= 1#
yields:
0≤a≤1
and:
#del y / del x#
yields:
![]()
and:
# partical x / partial t#
yields:
![]()
Digits, parentheses, brackets, punctuation marks, and the following mathematical words are converted into roman font instead of the italic font used for other text:

Summations, Integrals, Products, and Limits
Summations, integrals, products, and limits often require an upper and lower part around the symbol. The word from indicates the character sequence to be entered at the lower part; the word to indicates the upper part. These parts are both optional, but if they are used, they should appear in that order. For example, you would type:
#Expected~Value~=~sum from {i=l} to inf pi sub 1 X sub i#
to print the following expression:
![]()
Notice that we used braces around the from part although this was not neccessary because there were no imbedded blanks in the string i=l. But if the from and to parts contain any blanks to separate special words, you must use braces around them.
A from does not necessarily need an accompanying to, as you will see in the following example:
#lim from {m -> inf} sum from i=O to m c sup i#
which yields:
![]()
Square Root Signs
To draw a square root sign, use the word sqrt. For example:
#sqrt {b sup 2 − 4ac} #
yields:
![]()
Square roots of tall quantities appear too dark and heavy. Big square root quantities are better written to the power ½, as in:
2Co/D½
Creating a cube root or a higher root sign requires a little imagination. You can think of a cube root sign, for example, as consisting of two parts: a superscript 3 (with nothing before it) and a square root sign. However, you can’t type:
#sup 3 sqrt x#
because a sup is a superscript on something. You must use a pair of double quotation marks as a placeholder for sup. For example:
#"" sup 3 sqrt x#
yields:
![]()
Enclosing Braces and Brackets
You can generate big brackets [ ], braces { }, parentheses ( ), and bars I around quantities by using the words left and right, followed by the desired character. For example:
#P~=~R~left [ 1^-^{1+i sup n} over i right ]#
yields:
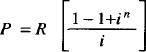
The resulting brackets (and any character you specify) are made big enough to enclose the quantity. (Braces are typically bigger than brackets and parentheses.) Note the spaces surrounding the words left and right and the character to be expanded.
Two other characters that you can use are the floor and ceiling characters shown in the following example:
#left floor a over b right floor !=
left ceiling x over y right ceiling#
which yields:
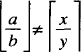
A left does not need a corresponding right. If the right part is omitted, use braces to enclose the quantity that you want the left bracket to cover. This is useful when you are making piles, as you will see in the next section.
You can also omit the left part, although technically you can’t have a right without an accompanying left. To get around this, you must type:
#left "" expression right ) #
The left "" in this equation means a “left nothing.”
▪ Other Positional Notation ▪
In addition to subscripts and superscripts, eqn lets you format expressions containing fractions, matrices, and vertical piles.
Fractions
Making a fraction, such as one-third, is as simple as typing “1 over 3.” For more complex fractions, eqn automatically positions the fraction bar and adjusts its length. Thus, the line:
#Income over Capital~=~Income over Sales~times~Sales over Capital#
yields:
![]()
When you have both a sup and an over in the same equation, eqn does sup before over. However, you can always use braces to tell eqn what part goes with what. For example, you would type:
#e sup {k over t]#
to yield:
![]()
You would not type:
#e sup k over t#
The latter form produces:
![]()
which is not what we want.
Arrays and Matrices
To make an array or a matrix, use the word matrix, and the words lcol, ccol, and rcol to denote the position of the columns. For example:
.EQ
matrix {
lcol {1 above 0}
rcol {half above −1)
}
.EN
yields:
1 1/2
0 −1
This produces a matrix with the first column left justified and the second column right justified. Each item is separated from the item below it by the word above. You can also center the columns using ccol. You can adjust each column separately and use as many columns as you like. However, each column must have the same number of items in it as the other columns.
A matrix should be used when the items in the columns don’t all have the same height (for example, when you have fractions mixed with whole numbers). This forces the items to line up because matrix looks at the entire structure before deciding what spacing to use.
Vertical Piles
To make vertical piles or columns of items, use the word pile before the equation description and the keyword above to separate the items. You can also enclose the piles in big braces or big brackets. For example:
.EQ
P~=~left [
pile ( nu sub 1 above nu sub 2 above cdot
above cdot above cdot above nu sub N }
right ]
. EN
yields:
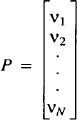
The items are centered one above the other and separated by the word above. Braces enclose the entire pile list. The items in the pile can themselves contain piles.
You can left justify (lpile), right justify (rpile), or center (cpile) the elements of the pile. (A cpile is the same as a regular pile.) However, the vertical spacing you get using these three forms will be somewhat larger than the normal pile. For example:
.EQ
f sub X (x) ^=^ left {
rpile { 0 above 2x above 0 }
~~lpile { x < 0 above 0 <= x <= 1 above x > 1 }
.EN
yields:
Note that in this example, we have a left brace without a corresponding right brace.
▪ Diacritical Marks ▪
With eqn, writing diacritical marks on top of letters is straightforward. The words known by eqn follow, with examples of how they appear on top of the letter x:

The following examples show how these keywords are used:
#cr e hat pes#
yields:
crêpes
and:
#Citr o dotdot en#
yields:
Citröen
and:
#a vec + b vec#
yields:
![]()
and:
#X bar sub st #
yields:
![]()
The eqn program positions the diacritical marks at the appropriate height. It also makes bar and under the right length to cover the entire item. Other marks are centered above the character(s).
Typing words with diacritical marks may seem confusing at first because you have to leave spaces around the letter and its corresponding mark. Just remember that eqn doesn’t print the spaces you type in.
▪ Defining Terms ▪
In some documents, you type a string of characters often, either within the text or within several equations. If you notice a string that is frequently used, you can name it using a define statement within an .EQ and .EN. Then you can use the name within an expression instead of typing the whole string.
Suppose you notice that the string 2 sup i appears repeatedly in equations. You can avoid retyping by naming it 2i, for example, as in the following commands:
.EQ
define 2i ’2 sup i’
.EN
You should enclose the string between single quotation marks or between any two characters that don’t appear inside the definition. After you’ve defined a term, you can use it as a convenient shorthand in other equations, just as if it were one of eqn’s special keywords.
A note about using definitions: although a definition can use a previous definition, do not define something in terms of itself. Thus:
.EQ
define 2i ‘2 sup i’
define 1/2i ‘1 over 2i’
.EN
is acceptable, but:
.EQ
define X ‘X bar’
.EN
is not because X is defined in terms of itself. If you want to do this, protect the X in the definition with double quotation marks, as in:
You can also redefine eqn keywords. For example, you can make / mean over by typing:
.EQ
define / ‘over’
.EN
▪ Quoted Text ▪
You have seen the use of double quotation marks as placeholders (in the sup, sqrt, and define examples) when eqn needs something grammatically but you don’t want anything in the output. Quotation marks are also used to get braces and other eqn keywords printed in the output. For example:
# ‘{ size beta }’ #
prints the words:
{size beta}
instead of looking up the two words size and beta in the eqn vocabulary and converting them. (The word size is used to change the size of the characters from the 10-point default.)
Any string entirely within quotation marks is not subject to font changes and spacing adjustments normally done by troff or nroff on the equation. This provides for individual spacing and adjusting, if needed. Thus, the line:
# italic “COS (x)” + cos (x) #
yields:
cos(x) +cos(x)
To print a literal quotation mark, you must escape it with a backslash character in the form \".
▪ Fine-Tuning the Document ▪
Typesetting a technical document is not only a matter of getting the eqn vocabulary right so you can print the appropriate mathematical expressions. Although eqn tries to make some actions automatic and puts items in the proper places, some fine-tuning is occasionally needed. With eqn, you can line up equations, define font sizes and types, and vary horizontal and vertical spacing.
Lining Up Equations
Earlier we showed you how to line up pieces of an equation using tabs. Another method of doing this is to use the commands mark and lineup. This is useful when you have to line up a series of equations at some horizontal position, often at an equal sign.
For example, you would type in:
.EQ
mu~mark =~lambda t
.EN
.EQ
lineup =~int from 0 to t lambda dz
.EN
to line up the two equations:
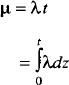
The word mark can appear only once at any place in an equation. Successive equations should also contain lineup only once. Thus, when you have a series of equations that require you to line up items in more than one position, like the following:

it might be better to line up the pieces of the equation on the left-hand side using tabs, and those on the right-hand side using mark and lineup.
If at all possible, you should type in the longest expression first to serve as the marking point. If you type in shorter expressions first, mark will not have enough room to line up successive longer expressions.
Changing Fonts and Sizes
In eqn, equations are automatically set in 10-point type, with standard mathematical conventions to write some characters as roman or italic. To change sizes and fonts, use the following keywords:
Like sup and sub, these keywords only apply to the character(s) immediately following them, and revert to the original size and font at the next space. To affect more complex or longer strings (such as a whole equation), use braces. Consider the following examples:
#bold qP# |
qp |
#roman alpha~beta# |
αβ |
#fat half# |
½ |
#size + 3 x =y# |
x =y |
#size 8 {A + B } # |
A +B |
If the entire paper is to be typeset in a nonstandard size or format, you can avoid redefining each and every character sequence by setting a global size (gsize) or font (gfont) that will affect the whole document. You can set this up at the top of your file (or wherever the font and size changes begin) within an .EQ and .EN.
For example, to change the fonts to roman and the size to 12, you could enter:
.EQ
gfont R
gsize 12
.EN
The rest of the equations in the document (up to another gfont or gsize) will be set in 12-point roman type. You can use any other troff font names in place of R.
Horizontal and Vertical Motions
You have already learned how to obtain small extra horizontal spaces in the output using ~ and ^. To move terms at some arbitrary length backward or forward, use the commands back n and fwd n, where n denotes how far you want to move, in 1/100s of an em. (An em is about the width of the letter m).
You can also move items up or down using up n or down n, where n is the same unit of measure as described. These local horizontal and vertical motions affect only the character(s) next to the keyword. To move larger strings or whole expressions, enclose them in braces.
▪ Keywords and Precedence ▪
Braces are used to group items or change the precedence of operations if you are unsure of how eqn will treat multiple keywords in a single expression. If you don’t use braces, eqn performs the operations in the following order:
dyad vec under bar tilde hat dot dotdot
fwd back down up
fat roman italic bold size
sub sup sqrt over
from to
All operations group to the right, except for the following, which group to the left:
over sqrt left right
▪ Problem Checklist ▪
The eqn program usually displays self-explanatory messages when it encounters a syntax error or any other formatting error. To check a document before printing, type:
$ eqn fies > /dev/null
This discards the output but prints the error message. Some of the error messages you might encounter are:
eqn : syntax error between lines 14 and 42, file book
A syntax error (such as leaving out a brace, having one too many braces, having a sup with nothing before it, or using a wrong delimiter) has occurred between lines 14 and 42, approximately, in the file book. These line numbers are not accurate, so you have to look at nearby lines as well. If the following message is displayed:
word overflow
you have exceeded the limits of troff’s internal buffer. If you print the equation as a displayed equation, this message will usually go away. If the message is line overflow, the only solution is to break up the equation across multiple lines, marking each with a separate .EQ and .EN. The eqn program does not warn about equations that are too long for one line. If the following message is displayed:
eqn : fatal error: Unexpected end of input at 2 sub a
you forgot to put a closing quotation mark after the string 2 sub a when you named it in the define statement.
It is also easy to leave out an ending delimiter in an equation. In this case, eqn thinks that successive character sequences (which may run to hundreds of lines) are still part of the inline expression. You may then get an overflow error or a garbled document. The checkeq program checks for misplaced or missing inline delimiters and similar problems.
For example, when run on a draft of this chapter, checkeq produced the following report:
$ checkeq sectl
sectl :
New delims ##, line 6
2 line ##, lines 618-619
2 line ##, lines 619-620
2 line ##, lines 620-621
.
.
.
EQ in ##, line 689
EN in ##, line 691
13 line ##, lines 709-721
.
.
.
2 line ##, lines 1300-1301
2 line ##, lines 1301-1302
Unfinished # #
This report (which ran to 66 lines) was telling us that somewhere before line 618 there was an unclosed inline equation using the delimeter #. Sure enough, the following error was found:
B#f( theta )
Because there was only one delimiter, eqn gets “out of phase” and all subsequent delimiters are misplaced. After we fixed this one error, checkeq printed the following “null” report:
$ checkeq sect1
sect 1 :
Because a simple problem like the one shown here can cause every subsequent equation in the file to be garbled, and can waste an entire formatting run, it makes sense to run checkeq before you format any files containing equations.
Get UNIX° TEXT PROCESSING now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.