VHF / UHF Filters and Multicouplers: Application of Air Resonators

Chapter 5

The Band-pass Filter

5.1. The band-pass function

Figure 5.1.

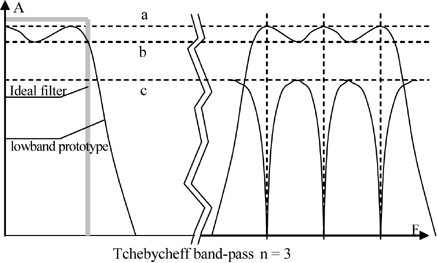
The ideal band-pass filter allows only a determined frequency band to pass, completely reflecting all the others; also has no losses and a constant group propagation time dφ/dω (phase is a linear function of the frequency). Real filters try to execute in the best possible way one or more of these characteristics, but never all of them at the same time, because the latter, at least, is achieved at the expense of the others and necessarily leads to a compromise. In order to help solve this problem, mathematical physicists have defined approximating functions that, as indicated by their name, allow a theoretical approach to the practical solution by means of modeling.

The most used approximating functions are those of Butterworth, Cauer (elliptical), Legendre, Gauss, Bessel, and above all Tchebycheff, a name well known in multiple spellings, which in fact covers a family of functions comprising a considerable number of variants. It is necessary in particular to distinguish the Tchebycheff polynomials from the rational functions of the same name, of which the polynomial is a particular case. Here we enter into details that are not really of interest to application engineers, but we will find, in case of necessity or mere curiosity, all the developments in the works of reference such as Zverev (see bibliography). ...