VLSI Digital Signal Processing Systems: Design and Implementation

13.6    CANONIC SIGNED DIGIT ARITHMETIC

The number of add operations required in a constant coefficient multiplication equals one less than the number of nonzero bits in the constant coefficient. In order to further reduce the area and power consumption, the constant coefficient can be encoded such that it contains the fewest number of nonzero bits, which can be accomplished using canonic signed digit (CSD) representation. Quantization of FIR digital filters using a specified number of signed power-of-two (SPT) terms is described in Appendix G.

This section addresses the CSD number representation and its applications for the design of bit-serial and bit-parallel constant multipliers.

13.6.1    CSD Representation

Consider the number A = a_W−1.a_W−2 … a₁a₀, where each a_i (W − 1 ≥ i ≥ 0) is in the set {−1, 0, 1}. Two’s complement representation may be considered as a special case, in which the bit a_W−1 is equal to 0 or −1, whereas a_i = 0 or 1 for 0 ≤ i ≤ W − 2. Now the multiplication A × X, where X is a variable, can be expressed as

where the number of additions/subtractions required equals one less than the number of nonzero bits in A. CSD representation is another special case, where no 2 consecutive a_i’s are nonzero.

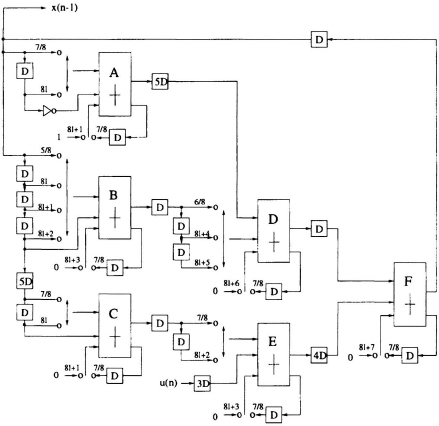
Fig. 13.29    Bit-serial architecture using two’s complement arithmetic. ...