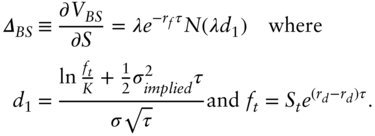CHAPTER 10The Black‐Scholes Greeks
This chapter discusses the many equations that follow from 
. I provide the BSM functional forms of the Greeks delta, forward delta, gamma, theta, vanna, and volgamma. I also introduce the concept of dual delta and use it to show how an option exposes the trader to the well‐known carry trade.
10.1 SPOT DELTA, DUAL DELTA, AND FORWARD DELTA
10.1.1 Spot Delta
The Black‐Scholes delta is calculated by differentiating Equation (9.12). I state the result before breaking it down into its components:
for a call option and 
for a put option. The intuition explaining the behavior of delta was captured by the simple model in (2.8) that showed that delta is the probability of an ITM expiry. This idea remains approximately true in the log‐normal BSM model. The feature box shows that the risk‐neutral probability of an ITM expiry in the BSM model is 
. Figure 10.1 plots for a reasonable range of real G10 FX market parameters showing that the difference is ...
Get Volatility now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
