Wavelets: Theory and Applications

2

The Discrete Wavelet Transform

The continuous theory in the previous chapter gave, in the main, an understanding of the ‘right’ interpretation of the wavelet transform. This chapter is concerned with the problems which arise if we wish to make hard calculations with the wavelet transform. These are

(a) the efficient calculation of the transform,

(b) the efficient reconstruction of signals from their transforms (inversion).

We attend to (b) first: this leads us to the concepts of frames and multiscale analysis, which elegantly solves (a).

2.1   Wavelet Frames

2.1.1 Introduction and Definition

A function f ∈ L² (ℝ) has the representation

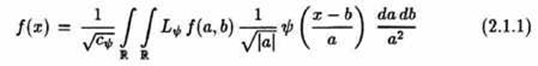
with the wavelet transform L_ψ for the wavelet ψ (cf. Theorem 1.1.9). Here we ask ourselves whether L_ψ f must be known at every point (a, b) ∈ ℝ\{0} × ℝ in order to work back to f. We largely suspect that the integral representation ( 2.1.1) is redundant and that therefore the integral can be replaced by a double sum without any loss of information.

Of course this will not hold for every wavelet and every discrete subset of ℝ\{0} × ℝ and we do not wish to generalize these wavelets and subsets. For this we refer to [DGM86, FG89a, FG89b, FG92, Grö93]. As an example we consider the lattice

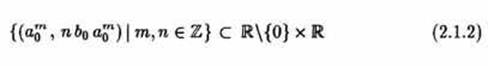
Figure 2.1 The distribution of phase-space points for a