Wavelets: Theory and Applications

3

Applications of the Wavelet Transform

3.1   Wavelet Analysis of One-Dimensional Signals

3.1.1 Preparations

At the heart of signal processing lies the task of extracting specific information from a signal s ∈ L²(ℝ), for example, the occurrence of certain patterns, periodic ranges, discontinuities, irregularities and other similar features. The wavelet transform can give a contribution to the answer to these questions whenever the sought phenomena show a multiscale structure. Typical examples are edges, jumps or locally varying orders of differentiability, which can easily be seen by the asymptotic behaviour of the wavelet transform. In contrast, a localization of discontinuities with the help of the classic Fourier transform is seldom possible. To this area belongs the analysis of the Riemann function, whose differentiability at certain points could be proved using wavelet analysis, cf. page 68.

In practice we deal not with analytic but discrete signals. We assume, then, that we are using the discrete values

of a measured signal. We adapt the situation to the conditions of the fast wavelet transform by carrying out two ‘preprocessing’ steps:

1. First we interpret the s_k as coefficients of a function  f ̃,

   

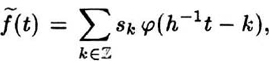
   expanded in terms of a scaling function φ. If φ has the interpolation property ...