Approximate Solution and Its Extension When Each Layer of a Two-Layer Reservoir Produces Independently (Chapter 7)☆
Suppose a homogeneous two-layer reservoir is penetrated by a well. Layer 1 and Layer 2 produce independently with constant dimensionless rates qD1 and qD2, respectively. The problem is expressed as follows:
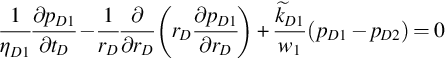
and
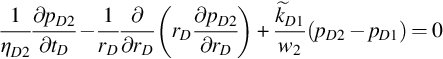 (E.1)
(E.1)
(E.2)
(E.3)
and
(E.4)
Using
Get Well Test Analysis for Multilayered Reservoirs with Formation Crossflow now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

