Wheeled Mobile Robotics

2.4 Dynamic Model of a Mobile System With Constraints

The kinematic model only describes static transformation of some robot velocities (pseudo velocities) to the velocities expressed in global coordinates. However, the dynamic motion model of the mechanical system includes dynamic properties such as system motion caused by external forces and system inertia. Using Lagrange formulation, which is especially suitable to describe mechanical systems [14], the dynamic model reads

$\begin{array}{l}\hfill \frac{d}{dt}\left(\frac{\partial \mathcal{L}}{\partial {\dot{q}}_k}\right)-\frac{\partial \mathcal{L}}{\partial q_k}+\frac{\partial P}{\partial {\dot{q}}_k}+g_k+{\tau }_{d_k}=f_k\end{array}$

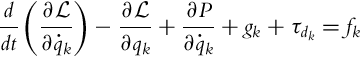  (2.46)

where index k describes the general coordinates q_k (k = 1, …, n), $\mathcal{L}$ defines the Lagrangian (difference between kinetic and potential ...