Acoustics: Sound Fields, Transducers and Vibration, 2nd Edition

12.8. Radiation from a piston in a sphere

The geometry of the piston of radius a in a sphere of radius R is shown in Fig. 12.22. In this example, we shall see the effect of having a planar radiator as opposed to the curved ones in all the previous examples. In the previous problem, the spherical cap followed the contour of the sphere so that there was only angular dependency in the velocity boundary condition with no radial dependency. This led to a direct solution for the expansion coefficients. Here, a flat circular piston [4] oscillates with a uniform axial velocity of u ˜ 0 . 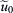Hence, the velocity boundary condition is more complicated ...