Advanced Numerical and Semi-Analytical Methods for Differential Equations

2Integral Transforms

2.1 Introduction

In Chapter 1, we have discussed about basic numerical methods by which one may find the approximate solutions of ordinary differential equations. In this regard, this chapter deals with the exact solutions of ordinary and partial differential equations. The methods we discuss here are integral transform methods. These are used frequently in different fields of engineering and sciences. Especially, Laplace transform (LT) and Fourier transform (FT) are having wide range of applications. Although one may find theories, concepts, and details about these methods in different excellent books [1–8]. But, just to have an idea of these methods, we introduce here the basic concepts of LT and FT. Accordingly, in this chapter, we will address these two methods LT and FT for solving ordinary and partial differential equations.

Integral transform of a function f(t) is defined as below:

(2.1)

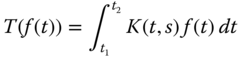
where K(t, s) is called kernel of the transformation.

2.2 Laplace Transform

LT is a well‐known integral transform method.

Definition 2.1

Let f(t) be a function of t for t ≥ 0, then LT of f(t) is defined as

(2.2)

where ℒ is the Laplacian operator.

In other way, one may define as below:

If the kernel in Eq. (2.1) is K(t, s) = e^−st, then the integral transform is called ...