Algorithms and Parallel Computing

17.4 FIELD MULTIPLICATION DEPENDENCE GRAPH

The iterations in Eq. 17.8 are defined over a two-dimensional (2-D) computation domain with the two indices i and j with the boundaries defined in Eq. 17.8. Since the dimensionality of is low, it is preferable to draw a dependence graph for the data and use the graphic and combinational geometric analysis tools discussed in Chapters 10 and 11. Figure 17.1 shows the dependence graph for the left-to-right shift-and-add field multiplication algorithm for m = 5. The algorithm has three input variables a, b and r and one output variable c.

Figure 17.1 Dependence graph for the left-to-right shift-and-add field multiplication algorithm for m = 5.

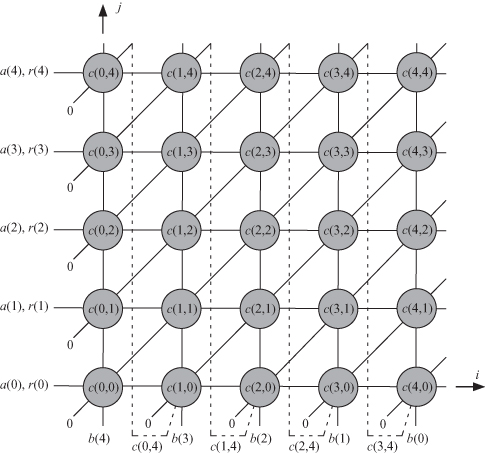
Input variables a(j) and r(j) will both map to horizontal lines. For example, input sample a(3) is associated with the line whose equation is i = 3. Also, a(j) or r(j) are fed to the system at one of two points (0, j) or (m − 1, j). We choose to feed the variable at the former point.

Input variable b(m − i) maps to vertical lines such that input instance b(3) maps to the line equation i = m − 3. Since in our case m = 5, instance b(3) maps to the line whose equation is i = 2 as shown in the figure. Also, ...