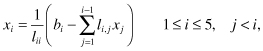April 2011
Intermediate to advanced
364 pages
10h 8m
English
Content preview from Algorithms and Parallel Computing
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.
20.3 FORWARD SUBSTITUTION (DIRECT TECHNIQUE)
The general form for a system of linear equations was given in Eq. 20.1. Forward substitution technique converts the square matrix A into a lower triangular form:
(20.10)
Consider the 5 × 5 lower triangular linear system:
(20.11)
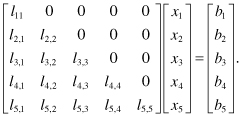
If all lii ≠ 0, then we can determine the unknowns according to the equations
where x1 must be calculated before x2 could be evaluated and so on. Thus, it appears that the calculations are sequential, with small opportunity for parallelization. However, the techniques we discussed earlier will help us derive parallel multithreaded and systolic architectures.
20.3.1 Forward Substitution Dependence Graph
The iterations in Eq. 20.12 use two indices i and j and we can use the results of Chapters 10 or 11 to study the parallelization of the forward substitution algorithm. Figure 20.1 is the dependence graph of the iterations in Eq. 20.12. Note that the variable x is an input/output variable and this explains why we have two sets of x, one set for the output instances of x and the other set is for the input instances of x.
Figure 20.1 The dependence graph of the forward substitution algorithm.
Input ...
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
and much more.
Read now
Unlock full access
More than 5,000 organizations count on O’Reilly
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.Julian F.
I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.Addison B.
I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.Amir M.
I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.