Analysis of Complex Networks

1.2 Entropy or the Information Content of Graphs

Given a decomposition of the vertices or edges of a graph, one can construct a finite probability scheme [10] and compute its entropy. A finite probability scheme assigns a probability to each subset in the decomposition. Such a numerical measure can be seen to capture the information contained in some particular aspect of the graph structure.

The orbits of the automorphism group of a graph constitute a decomposition of the vertices of the graph. As noted above, this decomposition captures the symmetry structure of the graph, and the entropy of the finite probability scheme obtained from the automorphism group provides an index of the complexity of the graph relative to the symmetry structure.

Let G = (V, E) be a graph with vertex set V (with |V | = n) and edge set E. The automorphism group of G, denoted by Aut(G), is the set of all adjacency preserving bijections of V. Let{V_i |1 ≤ i ≤ k} be the collection of orbits of Aut(G), and suppose |V_i | = n_i for 1 ≤ i ≤ k. The entropy or information content of G is given by the following formula ([13]):

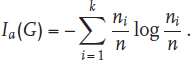
For example, the orbits of the graph of Figure 1.1 are {1}, {2,5}, and {3,4}, so the information content of the graph is .

Figure 1.1 Information content of a graph.

Clearly, I_a(G) satisfies ...