Analysis of Complex Networks

14.3 Classification of Elementary ({2, 3, 4, 5}, 3)-Polycycles

For 2 ≤ m ≤ ∞, denote by Barrel_m the ({5}, 3)-polycycle with two m-gonal holes separated by two m-rings of 5-gonal proper faces. This polycycle is nonextensible if and only if m ≥ 6. Its symmetry group, D_md, coincideswith the symmetry group of the underlying 3-valent plane graph if and only if m ≠ 5. See below for pictures of Barrel_m for m = 2, 3, 4, 5, and ∞:

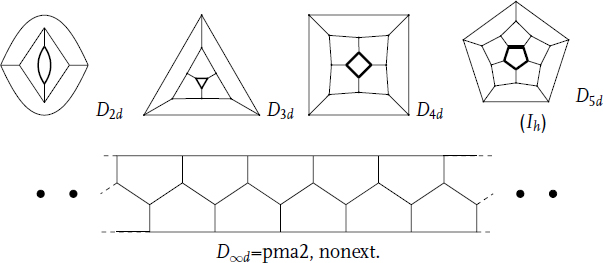
Theorem 14.3 The list of elementary ({2, 3, 4, 5},3)-polycycles consists of:

(i) 204 sporadic ({2, 3, 4, 5},3)_simp-polycycles, given in Appendix 1.

(ii) Six ({3, 4, 5},3)_simp-polycycles, infinite in one direction:

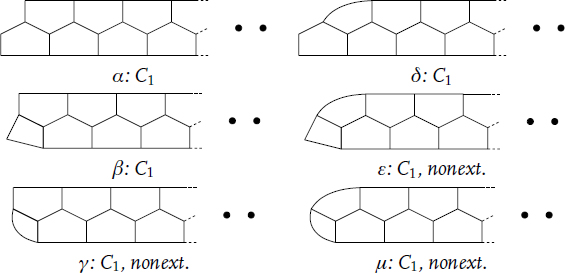
(iii) 21 = infinite series obtained by taking two ends of the infinite polycycles from (ii) above and concatenating them.

For example, merging α with itself produces the infinite series of elementary ({5},3)_simp-polycycles, denoted by E_n in [12]. See Figure 14.1 for the first 3 members (starting with 6 faces) of two such series: αα and βε.

(iv) The infinite series of Barrel_m, 2 ≤ m ≤ ∞, and its nonorientable quotient for m odd.

Proof. Take an elementary ({2, 3, 4, 5},3)_simp-polycycle P that, by Theorem 14.2, is kernel-elementary. If its kernel is empty, ...