14.5 Classification of Elementary ({2, 3}, 5)-Polycycles
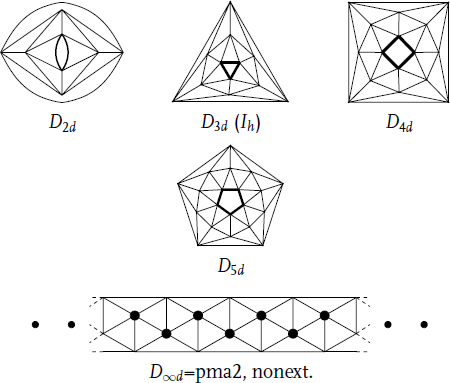
For 2 ≤ m ≤ ∞, call snub m-antiprism the ({3},5)simp-polycycle with two m-gonal holes separated by 4m 3-gonal proper faces. This polycycle is nonextensible if and only if m ≤ 4. Its symmetry group, Dmd, coincides with the symmetry group of an underlying 5-valent plane graph if and only if m =3. See below for pictures of a snub m-antiprism for m = 2, 3, 4, 5, and ∞ (see [4], p. 119 for a formal definition):
Theorem 14.5 The list of elementary ({2, 3},5)-polycycles consists of:
(i) 57 sporadic ({2, 3},5)simp-polycycles, given in Appendix 2.
(ii) The following 3 infinite ({2, 3},5)simp-polycycles:
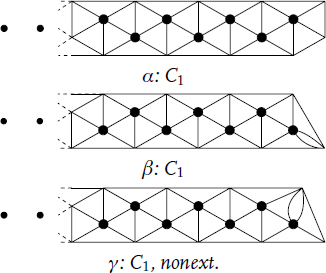
(iii) 6 infinite series of ({2, 3},5)simp-polycycles with one hole (obtained by concatenating endings of a pair of polycycles, given in (ii); see Figure 14.2 for the first 4 polycycles).
(iv) The infinite series of snub m-antiprisms for 2 ≤ m ≤ ∞ and its nonorientable quotient for m odd.
Proof. Take an elementary ({2, 3},5)simp-polycycle P that, by Proposition 14.2, is kernel-elementary. If its kernel is empty, then P is simply an r-gon with r ∈{2, 3}. If the kernel is reduced to a vertex, then P is simply a 5-tuple of 2-, 3-gons. If three edges ei = {vi–1, vi}, i =1,..., 3 are part of the kernel with e1, e2 and e2, e3 not part of an ...
Get Analysis of Complex Networks now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

