Analysis of Complex Networks

5.1 Motivation and Background

Random induced subgraphs arise in the context of molecular folding maps [24] where the neutral networks of molecular structures can be modeled as random induced subgraphs of n-cubes [17]. They also occur in the context of neutral evolution of populations (i.e., families of Qⁿ₂-vertices) consisting of erroneously replicating RNA strings. Here, one works in Qⁿ₄ since we have for RNA the nucleotides{A, U, G, C}. Random induced subgraphs of n-cubes have had an impact on the conceptual level [23] and led to experimental work identifying sequences that realize two distinct ribozymes [22]. A systematic computational analysis of neutral networks of molecular folding maps can be found in [11, 12]. An RNA structure, s, is a graph over [n] having vertex degree ≤ 1 and whose arcs are drawn in the upper half-plane (Figure 5.1). The set of s-compatible sequences, C[s], consists of all sequences that have at any two paired positions one of the 6 nucleotide pairs (A, U), (U, A), (G, U), (U, G), (G, C), (C, G). The structure s gives rise to a new adjacency relation within C[s]. Indeed, we can reorganize a sequence (x₁,..., x_n) into the tuple

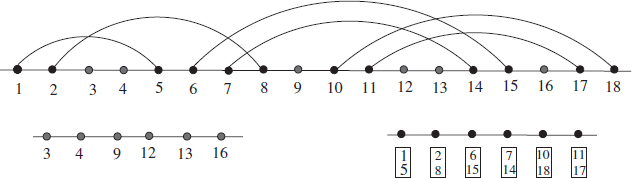
Figure 5.1 An RNA structure and its induced subcubes Q^nu ₄ and Q^np₆: a structure allows one to rearrange its compatible sequences into unpaired and paired segments. The former is a sequence over the original alphabet A, U, G,