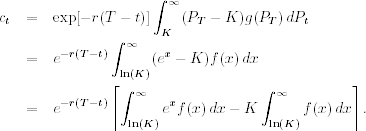Analysis of Financial Time Series, Third Edition

Appendix A: Integration of Black–Scholes Formula

In this appendix, we derive the price of a European call option given in Eq. (6.19). Let x = ln(PT). By changing variable and using g(PT) dPT = f(x) dx, where f(x) is the probability density function of x, we have

(6.36)

Because x = ln(PT) ∼ N[ln(Pt) + (r − σ2/2)(T − t), σ2(T − t)], the integration of the second term of Eq. (6.36) reduces to

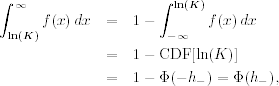
where CDF[ln(K)] is the cumulative distribution function (CDF) of x = ln(PT) evaluated at ln(K), Φ( · ) is the CDF of the standard normal random variable, and

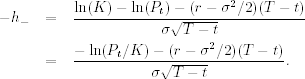
The integration of the first term of Eq. (6.36) can be written as

where the exponent can be simplified to

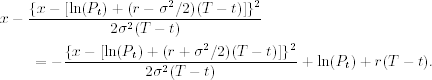
Consequently, the first integration becomes

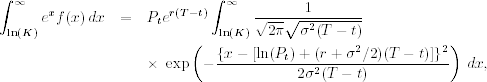
which involves the CDF of a normal distribution with mean ln(Pt) + (r + σ2/2)(T − t) and variance σ2(T − t). By using the same techniques as those of the second integration shown before, we have ...