Anomaly Detection for Monitoring

Chapter 4. Dealing with Trends and Seasonality

Trends and seasonality are two characteristics of time series metrics that break many models. In fact, they’re one of two major reasons why static thresholds break (the other is because systems are all different from each other). Trends are continuous increases or decreases in a metric’s value. Seasonality, on the other hand, reflects periodic (cyclical) patterns that occur in a system, usually rising above a baseline and then decreasing again. Common seasonal periods are hourly, daily, and weekly, but your systems may have a seasonal period that’s much longer or even some combination of different periods.

Another way to think about the effects of seasonality and trend is that they make it important to consider whether an anomaly is local or global. A local anomaly, for example, could be a spike during an idle period. It would not register as anomalously high overall, because it is still much lower than unusually high values during busy times. A global anomaly, in contrast, would be anomalously high (or low) no matter when it occurs. The goal is to be able to detect both kinds of anomalies. Clearly, static thresholds can only detect global anomalies when there’s seasonality or trend. Detecting local anomalies requires coping with these effects.

Many time series models, like the ARIMA family of models, have properties that handle trend. These models can also accomodate seasonality, with slight extensions.

Dealing with Trend

Trends break models because the value of a time series with a trend isn’t stable, or stationary, over time. Using a basic, fixed control chart on a time series with an increasing trend is a bad idea because it is guaranteed to eventually exceed the upper control limit.

A trend violates a lot of simple assumptions. What’s the mean of a metric that has a trend? There is no single value for the mean. Instead, the mean is actually a function with time as a parameter.

What about the distribution of values? You can visualize it using a histogram, but this is misleading. Because the values increase or decrease over time due to trend, the histogram will get wider and wider over time.

What about a simple moving average or a EWMA? A moving average should change along with the trend itself, and indeed it does. Unfortunately, this doesn’t work very well, because a moving average lags in the presence of a trend and will be consistently above or below the typical values.

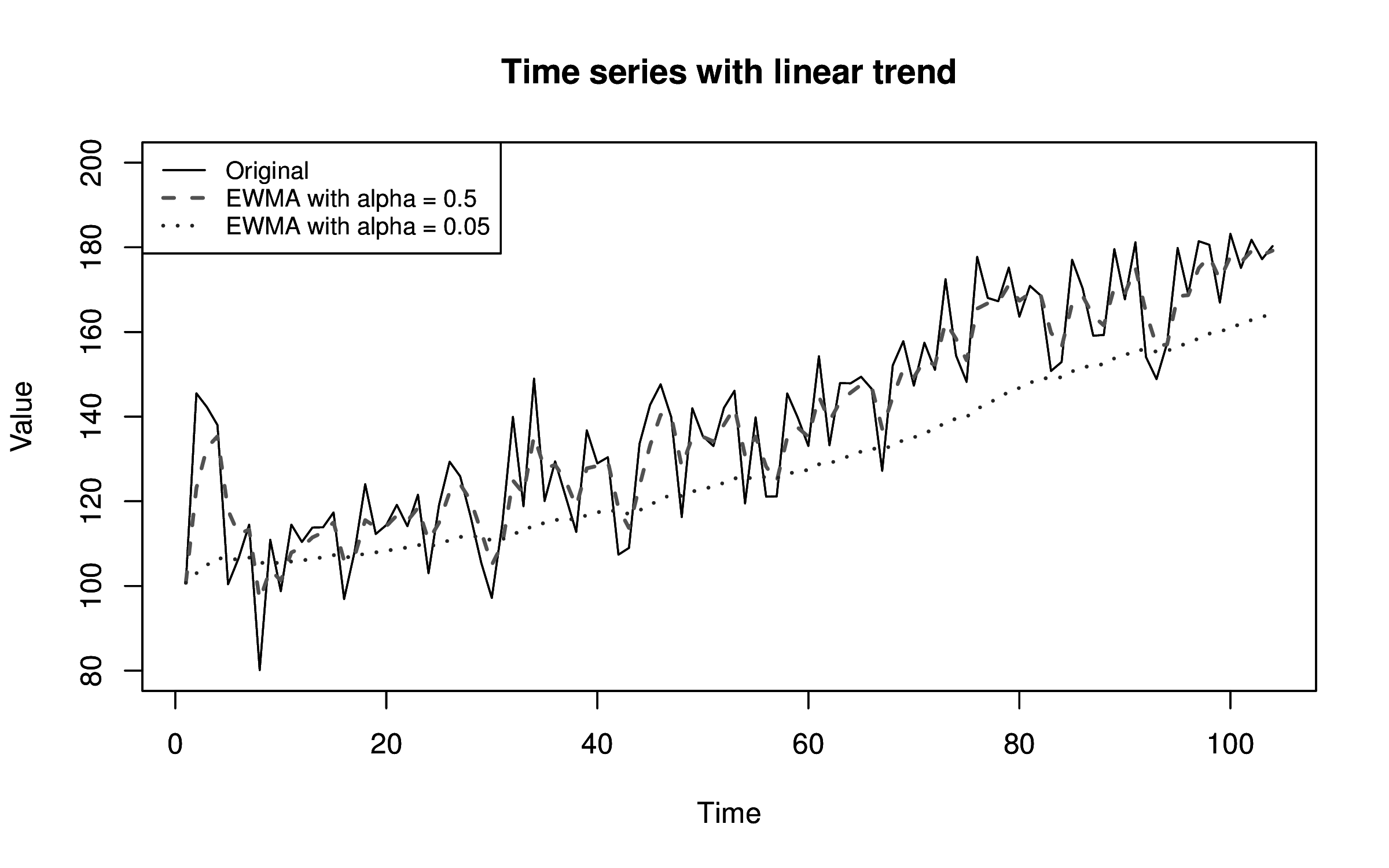
Figure 4-1. A time series with a linear trend and two exponentially weighted moving averages with different decay factors, demonstrating that they lag the data when it has a trend.

How do you deal with trend? First, it’s important to understand that metrics with trends can be considered as compositions of other metrics. One of the components is the trend, and so the solution to dealing with trend is simple: find a model that describes the trend, and subtract the trend from the metric’s values! After the trend is removed, you can use the models that we’ve previously mentioned on the remainder.

There can be many different kinds of trend, but linear is pretty common. This means a time series increases or decreases at a constant rate. To remove a linear trend, you can simply use a first difference. This means you consider the differences between consecutive values of a time series rather than the raw values of the time series itself. If you remember your calculus, this is related to a derivative, and in time series it’s pretty common to hear people talk about first differences as derivatives (or deltas).

Dealing with Seasonality

Seasonal time series data has cycles. These are usually obvious on observation, as shown in Figure 4-2.

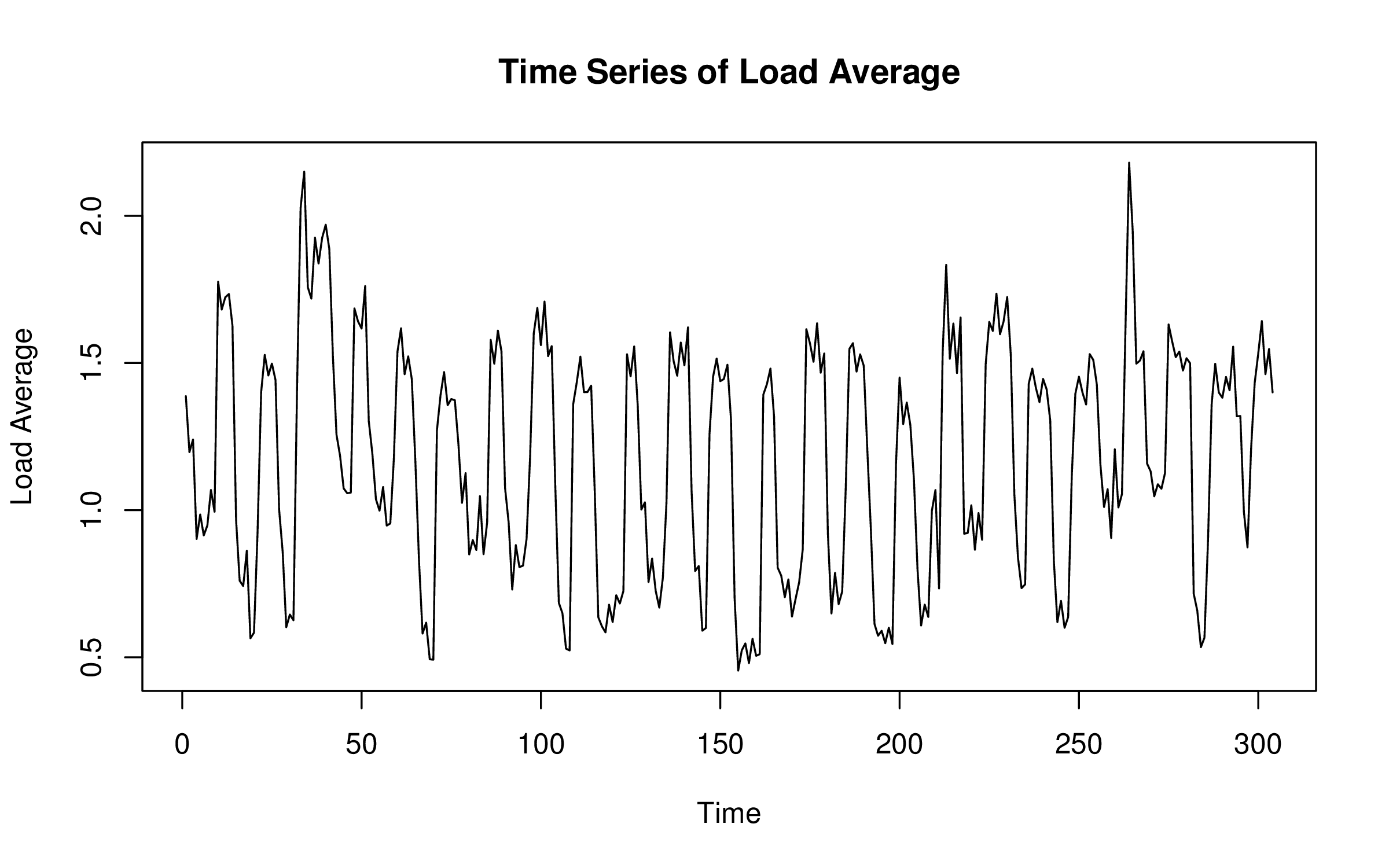
Figure 4-2. A server’s load average, showing repeated cycles over time.

Seasonality has very similar effects as trend. In fact, if you “zoom into” a time series with seasonality, it really looks like trend. That’s because seasonality is variable trend. Instead of increasing or decreasing at a fixed rate, a metric with seasonality increases or decreases with rates that vary with time. As you can imagine, things like EWMAs have the same issues as with linear trend. They lag behind, and in some cases it can get so bad that the EWMA is completely out of phase with the seasonal pattern. This is easy to see in Figure 4-3.

Figure 4-3. A sine wave and a EWMA of the sine wave, showing how a EWMA’s lag causes it to predict the wrong thing most of the time.

Coping with seasonality is exactly the same as with trend: you need to decompose and subtract. This time, however, it’s harder to do because the model of the seasonal component is much more complicated. Furthermore, there can be multiple seasonal components in a metric! For example, you can have a seasonal trend with a daily period as well as a weekly period.

Multiple Exponential Smoothing

Multiple exponential smoothing was introduced to resolve problems with using a EWMA on metrics with trend and/or seasonality. It offers an alternative approach: instead of modifying a metric to fit a model by decomposing it, it updates the model to fit the metric’s local behavior. Holt-Winters (also known as the Holt-Winters triple exponential smoothing method) is the best known implementation of this, and it’s what we’re going to focus on.

A multiple exponential smoothing model typically has up to three components: an EWMA, a trend component, and a seasonal component. The trend and seasonal components are EWMAs too. For example, the trend component is simply an EWMA of the differences between consecutive points. This is the same approach we talked about when discussing methods to deal with trend, but this time we’re doing it to the model instead of the original metric. With a single EWMA, there is a single smoothing factor: α (alpha). Because there are two more EWMAs for trend and seasonality, they also have their own smoothing factors. Typically they’re denoted as β (beta) for trend and γ (gamma) for seasonality.

Predicting the current value of a metric is similar to the previous models we’ve discussed, but with a slight modification. You start with the same “next = current” formula, but now you also have to add in the trend and seasonal terms. Multiple exponential smoothing usually produces much better results than naive models, in the presence of trend and seasonality.

Multiple exponential smoothing can get a little complicated to express in terms of mathematical formulas, but intuitively it isn’t so bad. We recommend the “Holt-Winters seasonal method” section¹ of the Forecasting: principles and practice for a detailed derivation. It definitely makes things harder, though:

• You have to know the period of the seasonality beforehand. The method can’t figure that out itself. If you don’t get this right, your model won’t be accurate and neither will your results.

• There are three EWMA smoothing parameters to pick. It becomes a delicate process to pick the right values for the parameters. Small changes in the parameters can create large changes in the predicted values. Many implementations use optimization techniques to figure out the parameters that work best on given sample data.

With that in mind, you can use multiple exponential smoothing to build SPC control charts just as we discussed in the previous chapter. The advantages and disadvantages are largely the same as we’ve seen before.

Potential Problems with Predicting Trend and Seasonality

In addition to being more complicated, advanced models that can handle trend and seasonality can still be problematic in some common situations. You can probably guess, for example, that outlying data can throw off future predictions, and that’s true, depending on the parameters you use:

• An outage can throw off a model by making it predict an outage again in the next cycle, which results in a false alarm.

• Holidays often aren’t in-sync with seasonality.

• There might be unusual events like Michael Jackson’s death. This actually might be something you want to be alerted on, but it’s clearly not a system fault or failure.

• There are annoying problems such as daylight saving time changes, especially across timezones and hemispheres.

In general, the Achilles heel of predictive models is the same thing that gives them their power: they can observe predictable behavior and predict it, but as a result they can be fooled into predicting the wrong thing. This depends on the parameters you use. Too sensitive and you get false positives; too robust and you miss them.

Another issue is that their predictive power operates at large time scales. In most systems you’re likely to work with, the seasonality is hourly, daily, and/or weekly. If you’re trying to predict things at higher resolutions, such as second by second, there’s so much mismatch between the time scales that they’re not very useful. Last week’s Monday morning spike of traffic may predict this morning’s spike pretty well in the abstract, but not down to the level of the second.

Fourier Transforms

It’s sometimes difficult to determine the seasonality of a metric. This is especially true with metrics that are compositions of multiple seasonal components. Fortunately, there’s a whole area of time series analysis that focuses on this topic: spectral analysis, which is the study of frequencies and their relative intensities. Within this field, there’s a very important function called the Fourier transform, which decomposes any signal (like a time series) into separate frequencies. This makes use of the very interesting fact that any signal can be broken up into individual sine waves.

The Fourier transform is used in many domains such as sound processing, to decompose, manipulate, and recombine frequencies that make up a signal. You’ll often hear people mention an FFT (Fast Fourier Transform). Perfectionists will point out that they probably mean a DFT (Discrete Fourier Transform).

Using a Fourier transform, it’s possible to take a very complicated time series with potentially many seasonal components, break them down into individual frequency peaks, and then subtract them from the original time series, keeping only the signal you want. Sounds great, pun intended! However, most machine data (unlike audio waves) is not really composed of strong frequencies. At least, it isn’t unless you look at it over long time ranges like weeks or months. Even then, only some metrics tend to have that kind of behavior.

One example of the Fourier transform in action is Netflix’s Scryer,² which is used to predict (or forecast) demand based on decomposed frequencies along with other methods. That said, we haven’t seen Fourier transforms used practically in anomaly detection per se. Scryer predicts, it doesn’t detect anomalies.

In our opinion, the useful things that can be done with a DFT, such as implementing low- or high-pass filters, can be done using much simpler methods. A low-pass filter can be implemented with a moving average, and a high-pass filter can be done with differencing.

Conclusions

Trend and seasonality throw monkey wrenches into lots of models, but they can often be handled fairly well by treating metrics as sums of several signals. Predicting a metric’s behavior then becomes a matter of decomposing the signals into their component parts, fitting models to the components, and subtracting the predictable components from the original.

Once you’ve done that, you have essentially gotten rid of the non-stationary parts of the signal, and, in theory, you should be able to apply standard techniques to the stationary signal that remains.

¹ https://www.otexts.org/fpp/7/5

² http://bit.ly/netflixscryer