Applied Text Analysis with Python

Chapter 4. Text Vectorization and Transformation Pipelines

Machine learning algorithms operate on a numeric feature space, expecting input as a two-dimensional array where rows are instances and columns are features. In order to perform machine learning on text, we need to transform our documents into vector representations such that we can apply numeric machine learning. This process is called feature extraction or more simply, vectorization, and is an essential first step toward language-aware analysis.

Representing documents numerically gives us the ability to perform meaningful analytics and also creates the instances on which machine learning algorithms operate. In text analysis, instances are entire documents or utterances, which can vary in length from quotes or tweets to entire books, but whose vectors are always of a uniform length. Each property of the vector representation is a feature. For text, features represent attributes and properties of documents—including its content as well as meta attributes, such as document length, author, source, and publication date. When considered together, the features of a document describe a multidimensional feature space on which machine learning methods can be applied.

For this reason, we must now make a critical shift in how we think about language—from a sequence of words to points that occupy a high-dimensional semantic space. Points in space can be close together or far apart, tightly clustered or evenly distributed. Semantic space is therefore mapped in such a way where documents with similar meanings are closer together and those that are different are farther apart. By encoding similarity as distance, we can begin to derive the primary components of documents and draw decision boundaries in our semantic space.

The simplest encoding of semantic space is the bag-of-words model, whose primary insight is that meaning and similarity are encoded in vocabulary. For example, the Wikipedia articles about baseball and Babe Ruth are probably very similar. Not only will many of the same words appear in both, they will not share many words in common with articles about casseroles or quantitative easing. This model, while simple, is extremely effective and forms the starting point for the more complex models we will explore.

In this chapter, we will demonstrate how to use the vectorization process to combine linguistic techniques from NLTK with machine learning techniques in Scikit-Learn and Gensim, creating custom transformers that can be used inside repeatable and reusable pipelines. By the end of this chapter, we will be ready to engage our preprocessed corpus, transforming documents to model space so that we can begin making predictions.

Words in Space

To vectorize a corpus with a bag-of-words (BOW) approach, we represent every document from the corpus as a vector whose length is equal to the vocabulary of the corpus. We can simplify the computation by sorting token positions of the vector into alphabetical order, as shown in Figure 4-1. Alternatively, we can keep a dictionary that maps tokens to vector positions. Either way, we arrive at a vector mapping of the corpus that enables us to uniquely represent every document.

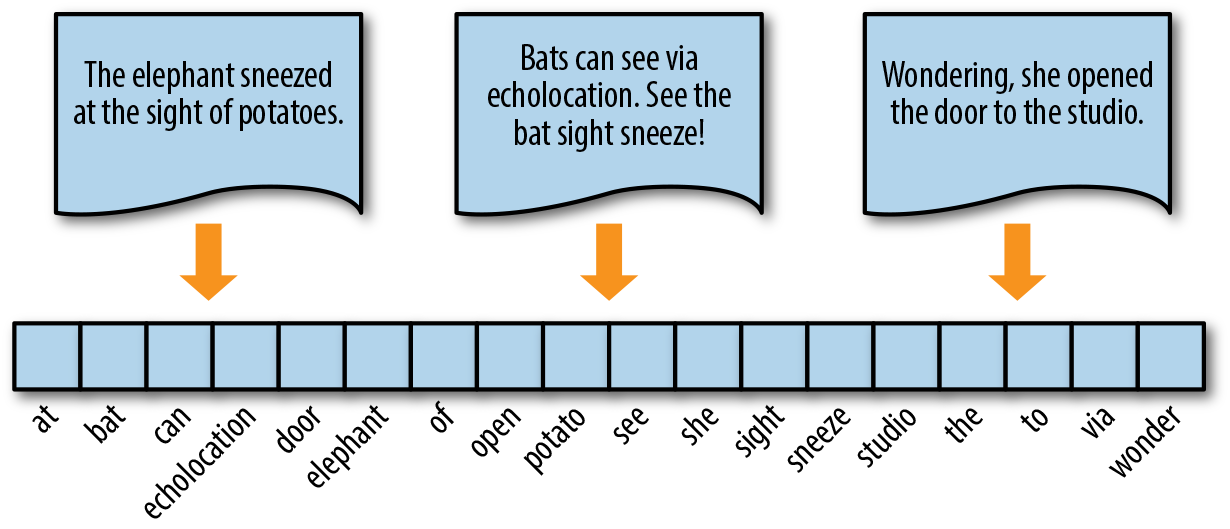
Figure 4-1. Encoding documents as vectors

What should each element in the document vector be? In the next few sections, we will explore several choices, each of which extends or modifies the base bag-of-words model to describe semantic space. We will look at four types of vector encoding—frequency, one-hot, TF–IDF, and distributed representations—and discuss their implementations in Scikit-Learn, Gensim, and NLTK. We’ll operate on a small corpus of the three sentences in the example figures.

To set this up, let’s create a list of our documents and tokenize them for the proceeding vectorization examples. The tokenize method performs some lightweight normalization, stripping punctuation using the string.punctuation character set and setting the text to lowercase. This function also performs some feature reduction using the SnowballStemmer to remove affixes such as plurality (“bats” and “bat” are the same token). The examples in the next section will utilize this example corpus and some will use the tokenization method.

import nltk
import string

def tokenize(text):
    stem = nltk.stem.SnowballStemmer('english')
    text = text.lower()

    for token in nltk.word_tokenize(text):
        if token in string.punctuation: continue
        yield stem.stem(token)

corpus = [
    "The elephant sneezed at the sight of potatoes.",
    "Bats can see via echolocation. See the bat sight sneeze!",
    "Wondering, she opened the door to the studio.",
]

The choice of a specific vectorization technique will be largely driven by the problem space. Similarly, our choice of implementation—whether NLTK, Scikit-Learn, or Gensim—should be dictated by the requirements of the application. For instance, NLTK offers many methods that are especially well-suited to text data, but is a big dependency. Scikit-Learn was not designed with text in mind, but does offer a robust API and many other conveniences (which we’ll explore later in this chapter) particularly useful in an applied context. Gensim can serialize dictionaries and references in matrix market format, making it more flexible for multiple platforms. However, unlike Scikit-Learn, Gensim doesn’t do any work on behalf of your documents for tokenization or stemming.

For this reason, as we walk through each of the four approaches to encoding, we’ll show a few options for implementation—“With NLTK,” “In Scikit-Learn,” and “The Gensim Way.”

Frequency Vectors

The simplest vector encoding model is to simply fill in the vector with the frequency of each word as it appears in the document. In this encoding scheme, each document is represented as the multiset of the tokens that compose it and the value for each word position in the vector is its count. This representation can either be a straight count (integer) encoding as shown in Figure 4-2 or a normalized encoding where each word is weighted by the total number of words in the document.

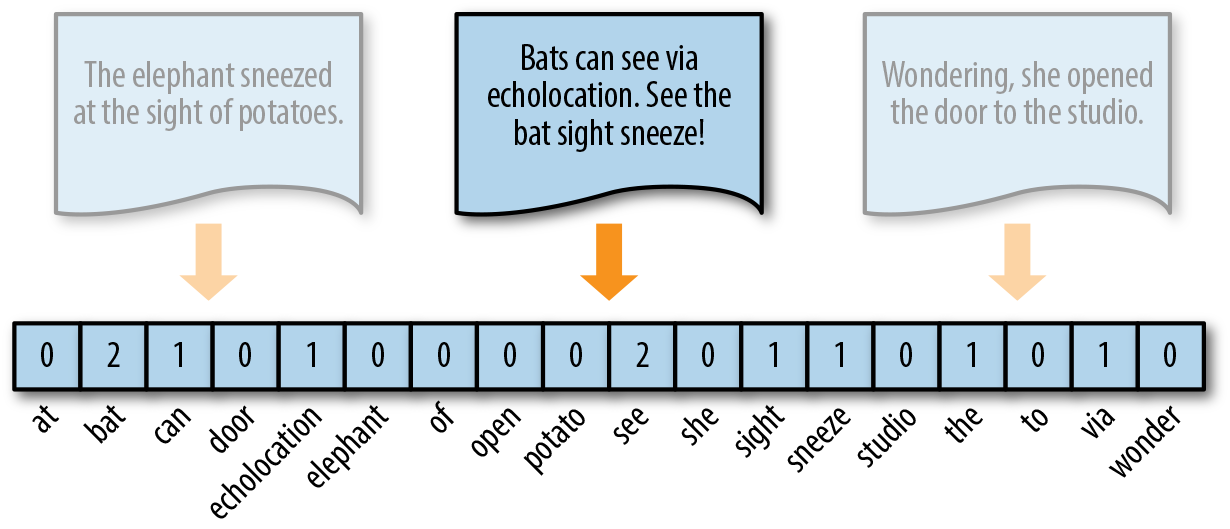
Figure 4-2. Token frequency as vector encoding

With NLTK

NLTK expects features as a dict object whose keys are the names of the features and whose values are boolean or numeric. To encode our documents in this way, we’ll create a vectorize function that creates a dictionary whose keys are the tokens in the document and whose values are the number of times that token appears in the document.

The defaultdict object allows us to specify what the dictionary will return for a key that hasn’t been assigned to it yet. By setting defaultdict(int) we are specifying that a 0 should be returned, thus creating a simple counting dictionary. We can map this function to every item in the corpus using the last line of code, creating an iterable of vectorized documents.

from collections import defaultdict

def vectorize(doc):
    features = defaultdict(int)
    for token in tokenize(doc):
        features[token] += 1
    return features

vectors = map(vectorize, corpus)

In Scikit-Learn

The CountVectorizer transformer from the sklearn.feature_extraction model has its own internal tokenization and normalization methods. The fit method of the vectorizer expects an iterable or list of strings or file objects, and creates a dictionary of the vocabulary on the corpus. When transform is called, each individual document is transformed into a sparse array whose index tuple is the row (the document ID) and the token ID from the dictionary, and whose value is the count:

from sklearn.feature_extraction.text import CountVectorizer

vectorizer = CountVectorizer()
vectors = vectorizer.fit_transform(corpus)

Note

Vectors can become extremely sparse, particularly as vocabularies get larger, which can have a significant impact on the speed and performance of machine learning models. For very large corpora, it is recommended to use the Scikit-Learn HashingVectorizer, which uses a hashing trick to find the token string name to feature index mapping. This means it uses very low memory and scales to large datasets as it does not need to store the entire vocabulary and it is faster to pickle and fit since there is no state. However, there is no inverse transform (from vector to text), there can be collisions, and there is no inverse document frequency weighting.

The Gensim way

Gensim’s frequency encoder is called doc2bow. To use doc2bow, we first create a Gensim Dictionary that maps tokens to indices based on observed order (eliminating the overhead of lexicographic sorting). The dictionary object can be loaded or saved to disk, and implements a doc2bow library that accepts a pretokenized document and returns a sparse matrix of (id, count) tuples where the id is the token’s id in the dictionary. Because the doc2bow method only takes a single document instance, we use the list comprehension to restore the entire corpus, loading the tokenized documents into memory so we don’t exhaust our generator:

import gensim

corpus  = [tokenize(doc) for doc in corpus]
id2word = gensim.corpora.Dictionary(corpus)
vectors = [
    id2word.doc2bow(doc) for doc in corpus
]

One-Hot Encoding

Because they disregard grammar and the relative position of words in documents, frequency-based encoding methods suffer from the long tail, or Zipfian distribution, that characterizes natural language. As a result, tokens that occur very frequently are orders of magnitude more “significant” than other, less frequent ones. This can have a significant impact on some models (e.g., generalized linear models) that expect normally distributed features.

A solution to this problem is one-hot encoding, a boolean vector encoding method that marks a particular vector index with a value of true (1) if the token exists in the document and false (0) if it does not. In other words, each element of a one-hot encoded vector reflects either the presence or absence of the token in the described text as shown in Figure 4-3.

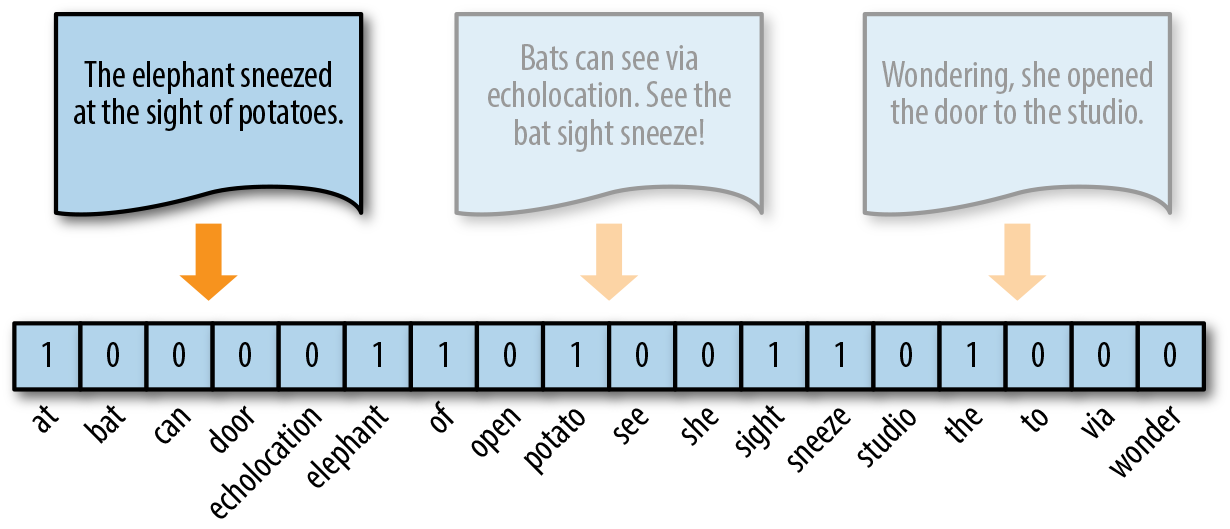
Figure 4-3. One-hot encoding

One-hot encoding reduces the imbalance issue of the distribution of tokens, simplifying a document to its constituent components. This reduction is most effective for very small documents (sentences, tweets) that don’t contain very many repeated elements, and is usually applied to models that have very good smoothing properties. One-hot encoding is also commonly used in artificial neural networks, whose activation functions require input to be in the discrete range of [0,1] or [-1,1].

With NLTK

The NLTK implementation of one-hot encoding is a dictionary whose keys are tokens and whose value is True:

def vectorize(doc):
    return {
        token: True
        for token in doc
    }

vectors = map(vectorize, corpus)

Dictionaries act as simple sparse matrices in the NLTK case because it is not necessary to mark every absent word False. In addition to the boolean dictionary values, it is also acceptable to use an integer value; 1 for present and 0 for absent.

In Scikit-Learn

In Scikit-Learn, one-hot encoding is implemented with the Binarizer transformer in the preprocessing module. The Binarizer takes only numeric data, so the text data must be transformed into a numeric space using the CountVectorizer ahead of one-hot encoding. The Binarizer class uses a threshold value (0 by default) such that all values of the vector that are less than or equal to the threshold are set to zero, while those that are greater than the threshold are set to 1. Therefore, by default, the Binarizer converts all frequency values to 1 while maintaining the zero-valued frequencies.

from sklearn.preprocessing import Binarizer

freq   = CountVectorizer()
corpus = freq.fit_transform(corpus)

onehot = Binarizer()
corpus = onehot.fit_transform(corpus.toarray())

The corpus.toarray() method is optional; it converts the sparse matrix representation to a dense one. In corpora with large vocabularies, the sparse matrix representation is much better. Note that we could also use CountVectorizer(binary=True) to achieve one-hot encoding in the above, obviating the Binarizer.

Caution

In spite of its name, the OneHotEncoder transformer in the sklearn.preprocessing module is not exactly the right fit for this task. The OneHotEncoder treats each vector component (column) as an independent categorical variable, expanding the dimensionality of the vector for each observed value in each column. In this case, the component (sight, 0) and (sight, 1) would be treated as two categorical dimensions rather than as a single binary encoded vector component.

The Gensim way

While Gensim does not have a specific one-hot encoder, its doc2bow method returns a list of tuples that we can manage on the fly. Extending the code from the Gensim frequency vectorization example in the previous section, we can one-hot encode our vectors with our id2word dictionary. To get our vectors, an inner list comprehension converts the list of tuples returned from the doc2bow method into a list of (token_id, 1) tuples and the outer comprehension applies that converter to all documents in the corpus:

corpus  = [tokenize(doc) for doc in corpus]
id2word = gensim.corpora.Dictionary(corpus)
vectors = [
    [(token[0], 1) for token in id2word.doc2bow(doc)]
    for doc in corpus
]

One-hot encoding represents similarity and difference at the document level, but because all words are rendered equidistant, it is not able to encode per-word similarity. Moreover, because all words are equally distant, word form becomes incredibly important; the tokens “trying” and “try” will be equally distant from unrelated tokens like “red” or “bicycle”! Normalizing tokens to a single word class, either through stemming or lemmatization, which we’ll explore later in this chapter, ensures that different forms of tokens that embed plurality, case, gender, cardinality, tense, etc., are treated as single vector components, reducing the feature space and making models more performant.

Term Frequency–Inverse Document Frequency

The bag-of-words representations that we have explored so far only describe a document in a standalone fashion, not taking into account the context of the corpus. A better approach would be to consider the relative frequency or rareness of tokens in the document against their frequency in other documents. The central insight is that meaning is most likely encoded in the more rare terms from a document. For example, in a corpus of sports text, tokens such as “umpire,” “base,” and “dugout” appear more frequently in documents that discuss baseball, while other tokens that appear frequently throughout the corpus, like “run,” “score,” and “play,” are less important.

TF–IDF, term frequency–inverse document frequency, encoding normalizes the frequency of tokens in a document with respect to the rest of the corpus. This encoding approach accentuates terms that are very relevant to a specific instance, as shown in Figure 4-4, where the token studio has a higher relevance to this document since it only appears there.

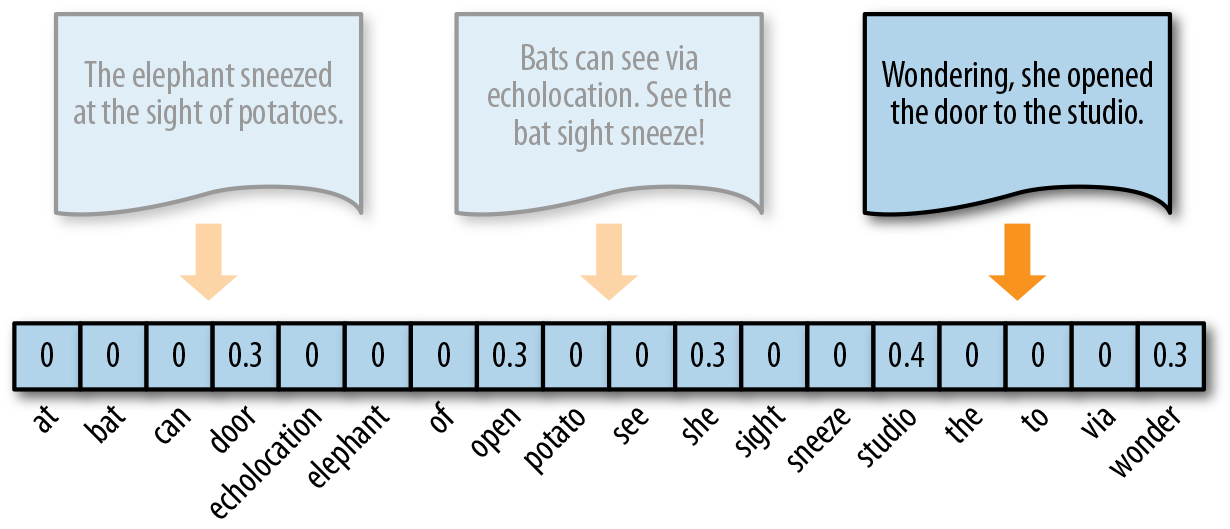
Figure 4-4. TF–IDF encoding

TF–IDF is computed on a per-term basis, such that the relevance of a token to a document is measured by the scaled frequency of the appearance of the term in the document, normalized by the inverse of the scaled frequency of the term in the entire corpus.

Computing TF–IDF

The term frequency of a term given a document, $tf(t,d)$, can be the boolean frequency (as in one-hot encoding, 1 if $t$ occurs in $d$ 0 otherwise), or the count. However, generally both the term frequency and inverse document frequency are scaled logarithmically to prevent bias of longer documents or terms that appear much more frequently relative to other terms: $tf(t,d)=1+log{f}_{t,d}$.

Similarly, the inverse document frequency of a term given the set of documents can be logarithmically scaled as follows: $idf(t,D)=log1+\frac{N}{n_t}$, where $N$ is the number of documents and $n_t$ is the number of occurrences of the term $t$ in all documents. TF–IDF is then computed completely as $tfidf(t,d,D)=tf(t,d)·idf(t,D)$.

Because the ratio of the id f log function is greater or equal to 1, the TF–IDF score is always greater than or equal to zero. We interpret the score to mean that the closer the TF–IDF score of a term is to 1, the more informative that term is to that document. The closer the score is to zero, the less informative that term is.

With NLTK

To vectorize text in this way with NLTK, we use the TextCollection class, a wrapper for a list of texts or a corpus consisting of one or more texts. This class provides support for counting, concordancing, collocation discovery, and more importantly, computing tf_idf.

Because TF–IDF requires the entire corpus, our new version of vectorize does not accept a single document, but rather all documents. After applying our tokenization function and creating the text collection, the function goes through each document in the corpus and yields a dictionary whose keys are the terms and whose values are the TF–IDF score for the term in that particular document.

from nltk.text import TextCollection

def vectorize(corpus):
    corpus = [tokenize(doc) for doc in corpus]
    texts  = TextCollection(corpus)

    for doc in corpus:
        yield {
            term: texts.tf_idf(term, doc)
            for term in doc
        }

In Scikit-Learn

Scikit-Learn provides a transformer called the TfidfVectorizer in the module called feature_extraction.text for vectorizing documents with TF–IDF scores. Under the hood, the TfidfVectorizer uses the CountVectorizer estimator we used to produce the bag-of-words encoding to count occurrences of tokens, followed by a TfidfTransformer, which normalizes these occurrence counts by the inverse document frequency.

The input for a TfidfVectorizer is expected to be a sequence of filenames, file-like objects, or strings that contain a collection of raw documents, similar to that of the CountVectorizer. As a result, a default tokenization and preprocessing method is applied unless other functions are specified. The vectorizer returns a sparse matrix representation in the form of ((doc, term), tfidf) where each key is a document and term pair and the value is the TF–IDF score.

from sklearn.feature_extraction.text import TfidfVectorizer

tfidf  = TfidfVectorizer()
corpus = tfidf.fit_transform(corpus)

The Gensim way

In Gensim, the TfidfModel data structure is similar to the Dictionary object in that it stores a mapping of terms and their vector positions in the order they are observed, but additionally stores the corpus frequency of those terms so it can vectorize documents on demand. As before, Gensim allows us to apply our own tokenization method, expecting a corpus that is a list of lists of tokens. We first construct the lexicon and use it to instantiate the TfidfModel, which computes the normalized inverse document frequency. We can then fetch the TF–IDF representation for each vector using a getitem, dictionary-like syntax, after applying the doc2bow method to each document using the lexicon.

corpus  = [tokenize(doc) for doc in corpus]
lexicon = gensim.corpora.Dictionary(corpus)
tfidf   = gensim.models.TfidfModel(dictionary=lexicon, normalize=True)
vectors = [tfidf[lexicon.doc2bow(doc)] for doc in corpus]

Gensim provides helper functionality to write dictionaries and models to disk in a compact format, meaning you can conveniently save both the TF–IDF model and the lexicon to disk in order to load them later to vectorize new documents. It is possible (though slightly more work) to achieve the same result by using the pickle module in combination with Scikit-Learn. To save a Gensim model to disk:

lexicon.save_as_text('lexicon.txt', sort_by_word=True)
tfidf.save('tfidf.pkl')

This will save the lexicon as a text-delimited text file, sorted lexicographically, and the TF–IDF model as a pickled sparse matrix. Note that the Dictionary object can also be saved more compactly in a binary format using its save method, but save_as_text allows easy inspection of the dictionary for later work. To load the models from disk:

lexicon = gensim.corpora.Dictionary.load_from_text('lexicon.txt')
tfidf = gensim.models.TfidfModel.load('tfidf.pkl')

One benefit of TF–IDF is that it naturally addresses the problem of stopwords, those words most likely to appear in all documents in the corpus (e.g., “a,” “the,” “of”, etc.), and thus will accrue very small weights under this encoding scheme. This biases the TF–IDF model toward moderately rare words. As a result TF–IDF is widely used for bag-of-words models, and is an excellent starting point for most text analytics.

Distributed Representation

While frequency, one-hot, and TF–IDF encoding enable us to put documents into vector space, it is often useful to also encode the similarities between documents in the context of that same vector space. Unfortunately, these vectorization methods produce document vectors with non-negative elements, which means we won’t be able to compare documents that don’t share terms (because two vectors with a cosine distance of 1 will be considered far apart, even if they are semantically similar).

When document similarity is important in the context of an application, we instead encode text along a continuous scale with a distributed representation, as shown in Figure 4-5. This means that the resulting document vector is not a simple mapping from token position to token score. Instead, the document is represented in a feature space that has been embedded to represent word similarity. The complexity of this space (and the resulting vector length) is the product of how the mapping to that representation is learned. The complexity of this space (and the resulting vector length) is the product of how that representation is trained and not directly tied to the document itself.

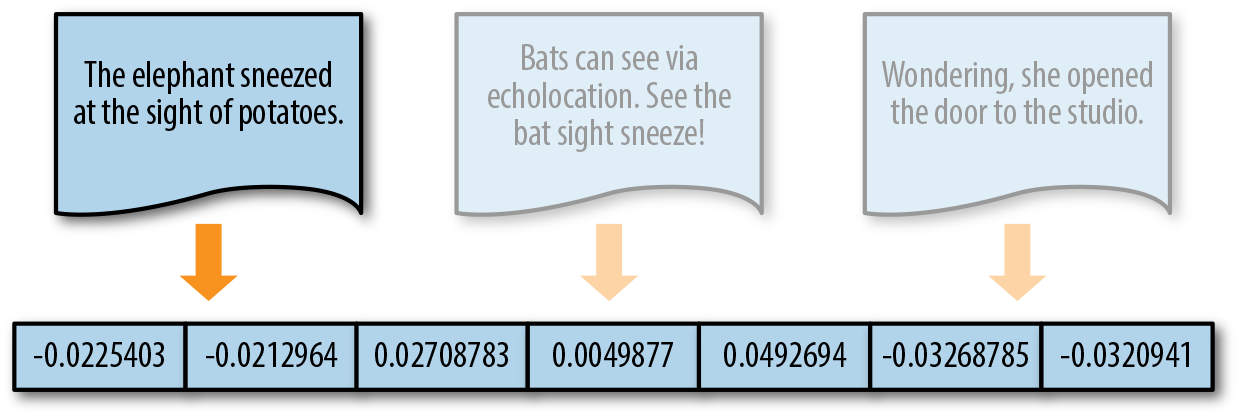
Figure 4-5. Distributed representation

Word2vec, created by a team of researchers at Google led by Tomáš Mikolov, implements a word embedding model that enables us to create these kinds of distributed representations. The word2vec algorithm trains word representations based on either a continuous bag-of-words (CBOW) or skip-gram model, such that words are embedded in space along with similar words based on their context. For example, Gensim’s implementation uses a feedforward network.

The doc2vec¹ algorithm is an extension of word2vec. It proposes a paragraph vector—an unsupervised algorithm that learns fixed-length feature representations from variable length documents. This representation attempts to inherit the semantic properties of words such that “red” and “colorful” are more similar to each other than they are to “river” or “governance.” Moreover, the paragraph vector takes into consideration the ordering of words within a narrow context, similar to an n-gram model. The combined result is much more effective than a bag-of-words or bag-of-n-grams model because it generalizes better and has a lower dimensionality but still is of a fixed length so it can be used in common machine learning algorithms.

The Gensim way

Neither NLTK nor Scikit-Learn provide implementations of these kinds of word embeddings. Gensim’s implementation allows users to train both word2vec and doc2vec models on custom corpora and also conveniently comes with a model that is pretrained on the Google news corpus.

Note

To use Gensim’s pretrained models, you’ll need to download the model bin file, which clocks in at 1.5 GB. For applications that require extremely lightweight dependencies (e.g., if they have to run on an AWS lambda instance), this may not be practicable.

We can train our own model as follows. First, we use a list comprehension to load our corpus into memory. (Gensim supports streaming, but this will enable us to avoid exhausting the generator.) Next, we create a list of TaggedDocument objects, which extend the LabeledSentence, and in turn the distributed representation of word2vec. TaggedDocument objects consist of words and tags. We can instantiate the tagged document with the list of tokens along with a single tag, one that uniquely identifies the instance. In this example, we’ve labeled each document as "d{}".format(idx), e.g. d0, d1, d2 and so forth.

Once we have a list of tagged documents, we instantiate the Doc2Vec model and specify the size of the vector as well as the minimum count, which ignores all tokens that have a frequency less than that number. The size parameter is usually not as low a dimensionality as 5; we selected such a small number for demonstration purposes only. We also set the min_count parameter to zero to ensure we consider all tokens, but generally this is set between 3 and 5, depending on how much information the model needs to capture. Once instantiated, an unsupervised neural network is trained to learn the vector representations, which can then be accessed via the docvecs property.

from gensim.models.doc2vec import TaggedDocument, Doc2Vec

corpus = [list(tokenize(doc)) for doc in corpus]
corpus = [
    TaggedDocument(words, ['d{}'.format(idx)])
    for idx, words in enumerate(corpus)
]

model = Doc2Vec(corpus, size=5, min_count=0)
print(model.docvecs[0])
# [ 0.01797447 -0.01509272  0.0731937   0.06814702 -0.0846546 ]

Distributed representations will dramatically improve results over TF–IDF models when used correctly. The model itself can be saved to disk and retrained in an active fashion, making it extremely flexible for a variety of use cases. However, on larger corpora, training can be slow and memory intensive, and it might not be as good as a TF–IDF model with Principal Component Analysis (PCA) or Singular Value Decomposition (SVD) applied to reduce the feature space. In the end, however, this representation is breakthrough work that has led to a dramatic improvement in text processing capabilities of data products in recent years.

Again, the choice of vectorization technique (as well as the library implementation) tend to be use case- and application-specific, as summarized in Table 4-1.

Table 4-1. Overview of text vectorization methods

Vectorization Method	Function	Good For	Considerations
Frequency	Counts term frequencies	Bayesian models	Most frequent words not always most informative
One-Hot Encoding	Binarizes term occurrence (0, 1)	Neural networks	All words equidistant, so normalization extra important
TF–IDF	Normalizes term frequencies across documents	General purpose	Moderately frequent terms may not be representative of document topics
Distributed Representations	Context-based, continuous term similarity encoding	Modeling more complex relationships	Performance intensive; difficult to scale without additional tools (e.g., Tensorflow)

Later in this chapter we will explore the Scikit-Learn Pipeline object, which enables us to streamline vectorization together with later modeling phrases. As such, we often prefer to use vectorizers that conform to the Scikit-Learn API. In the next section, we will discuss how the API is organized and demonstrate how to integrate vectorization into a complete pipeline to construct the core of a fully operational (and customizable!) textual machine learning application.

The Scikit-Learn API

Scikit-Learn is an extension of SciPy (a scikit) whose primary purpose is to provide machine learning algorithms as well as the tools and utilities required to engage in successful modeling. Its primary contribution is an “API for machine learning” that exposes the implementations of a wide array of model families into a single, user-friendly interface. The result is that Scikit-Learn can be used to simultaneously train a staggering variety of models, evaluate and compare them, and then utilize the fitted model to make predictions on new data. Because Scikit-Learn provides a standardized API, this can be done with little effort and models can be prototyped and evaluated by simply swapping out a few lines of code.

The BaseEstimator Interface

The API itself is object-oriented and describes a hierarchy of interfaces for different machine learning tasks. The root of the hierarchy is an Estimator, broadly any object that can learn from data. The primary Estimator objects implement classifiers, regressors, or clustering algorithms. However, they can also include a wide array of data manipulation, from dimensionality reduction to feature extraction from raw data. The Estimator essentially serves as an interface, and classes that implement Estimator functionality must have two methods—fit and predict—as shown here:

from sklearn.base import BaseEstimator

class Estimator(BaseEstimator):

    def fit(self, X, y=None):
        """
        Accept input data, X, and optional target data, y. Returns self.
        """
        return self

    def predict(self, X):
        """
        Accept input data, X and return a vector of predictions for each row.
        """
        return yhat

The Estimator.fit method sets the state of the estimator based on the training data, X and y. The training data X is expected to be matrix-like—for example, a two-dimensional NumPy array of shape (n_samples, n_features) or a Pandas DataFrame whose rows are the instances and whose columns are the features. Supervised estimators are also fit with a one-dimensional NumPy array, y, that holds the correct labels. The fitting process modifies the internal state of the estimator such that it is ready or able to make predictions. This state is stored in instance variables that are usually postfixed with an underscore (e.g., Estimator.coefs_). Because this method modifies an internal state, it returns self so the method can be chained.

The Estimator.predict method creates predictions using the internal, fitted state of the model on the new data, X. The input for the method must have the same number of columns as the training data passed to fit, and can have as many rows as predictions are required. This method returns a vector, yhat, which contains the predictions for each row in the input data.

Note

Extending Scikit-Learn’s BaseEstimator automatically gives the Estimator a fit_predict method, which allows you to combine fit and predict in one simple call.

Estimator objects have parameters (also called hyperparameters) that define how the fitting process is conducted. These parameters are set when the Estimator is instantiated (and if not specified, they are set to reasonable defaults), and can be modified with the get_param and set_param methods that are also available from the BaseEstimator super class.

We engage the Scikit-Learn API by specifying the package and type of the estimator. Here we select the Naive Bayes model family, and a specific member of the family, a multinomial model (which is suitable for text classification). The model is defined when the class is instantiated and hyperparameters are passed in. Here we pass an alpha parameter that is used for additive smoothing, as well as prior probabilities for each of our two classes. The model is trained on specific data (documents and labels) and at that point becomes a fitted model. This basic usage is the same for every model (Estimator) in Scikit-Learn, from random forest decision tree ensembles to logistic regressions and beyond.

from sklearn.naive_bayes import MultinomialNB

model = MultinomialNB(alpha=0.0, class_prior=[0.4, 0.6])
model.fit(documents, labels)

Extending TransformerMixin

Scikit-Learn also specifies utilities for performing machine learning in a repeatable fashion. We could not discuss Scikit-Learn without also discussing the Transformer interface. A Transformer is a special type of Estimator that creates a new dataset from an old one based on rules that it has learned from the fitting process. The interface is as follows:

from sklearn.base import TransformerMixin

class Transfomer(BaseEstimator, TransformerMixin):

    def fit(self, X, y=None):
        """
        Learn how to transform data based on input data, X.
        """
        return self

    def transform(self, X):
        """
        Transform X into a new dataset, Xprime and return it.
        """
        return Xprime

The Transformer.transform method takes a dataset and returns a new dataset, X`, with new values based on the transformation process. There are several transformers included in Scikit-Learn, including transformers to normalize or scale features, handle missing values (imputation), perform dimensionality reduction, extract or select features, or perform mappings from one feature space to another.

Although both NLTK, Gensim, and even newer text analytics libraries like SpaCy have their own internal APIs and learning mechanisms, the scope and comprehensiveness of Scikit-Learn models and methodologies for machine learning make it an essential part of the modeling workflow. As a result, we propose to use the API to create our own Transformer and Estimator objects that implement methods from NLTK and Gensim. For example, we can create topic modeling estimators that wrap Gensim’s LDA and LSA models (which are not currently included in Scikit-Learn) or create transformers that utilize NLTK’s part-of-speech tagging and named entity chunking methods.

Creating a custom Gensim vectorization transformer

Gensim vectorization techniques are an interesting case study because Gensim corpora can be saved and loaded from disk in such a way as to remain decoupled from the pipeline. However, it is possible to build a custom transformer that uses Gensim vectorization. Our GensimVectorizer transformer will wrap a Gensim Dictionary object generated during fit() and whose doc2bow method is used during transform(). The Dictionary object (like the TfidfModel) can be saved and loaded from disk, so our transformer utilizes that methodology by taking a path on instantiation. If a file exists at that path, it is loaded immediately. Additionally, a save() method allows us to write our Dictionary to disk, which we can do in fit().

The fit() method constructs the Dictionary object by passing already tokenized and normalized documents to the Dictionary constructor. The Dictionary is then immediately saved to disk so that the transformer can be loaded without requiring a refit. The transform() method uses the Dictionary.doc2bow method, which returns a sparse representation of the document as a list of (token_id, frequency) tuples. This representation can present challenges with Scikit-Learn, however, so we utilize a Gensim helper function, sparse2full, to convert the sparse representation into a NumPy array.

import os
from gensim.corpora import Dictionary
from gensim.matutils import sparse2full

class GensimVectorizer(BaseEstimator, TransformerMixin):

    def __init__(self, path=None):
        self.path = path
        self.id2word = None
        self.load()

    def load(self):
        if os.path.exists(self.path):
            self.id2word = Dictionary.load(self.path)

    def save(self):
        self.id2word.save(self.path)

    def fit(self, documents, labels=None):
        self.id2word = Dictionary(documents)
        self.save()
            return self

    def transform(self, documents):
        for document in documents:
            docvec = self.id2word.doc2bow(document)
            yield sparse2full(docvec, len(self.id2word))

It is easy to see how the vectorization methodologies that we discussed earlier in the chapter can be wrapped by Scikit-Learn transformers. This gives us more flexibility in the approaches we take, while still allowing us to leverage the machine learning utilities in each library. We will leave it to the reader to extend this example and investigate TF–IDF and distributed representation transformers that are implemented in the same fashion.

Creating a custom text normalization transformer

Many model families suffer from “the curse of dimensionality”; as the feature space increases in dimensions, the data becomes more sparse and less informative to the underlying decision space. Text normalization reduces the number of dimensions, decreasing sparsity. Besides the simple filtering of tokens (removing punctuation and stopwords), there are two primary methods for text normalization: stemming and lemmatization.

Stemming uses a series of rules (or a model) to slice a string to a smaller substring. The goal is to remove word affixes (particularly suffixes) that modify meaning. For example, removing an 's' or 'es', which generally indicates plurality in Latin languages. Lemmatization, on the other hand, uses a dictionary to look up every token and returns the canonical “head” word in the dictionary, called a lemma. Because it is looking up tokens from a ground truth, it can handle irregular cases as well as handle tokens with different parts of speech. For example, the verb 'gardening' should be lemmatized to 'to garden', while the nouns 'garden' and 'gardener' are both different lemmas. Stemming would capture all of these tokens into a single 'garden' token.

Stemming and lemmatization have their advantages and disadvantages. Because it only requires us to splice word strings, stemming is faster. Lemmatization, on the other hand, requires a lookup to a dictionary or database, and uses part-of-speech tags to identify a word’s root lemma, making it noticeably slower than stemming, but also more effective.

To perform text normalization in a systematic fashion, we will write a custom transformer that puts these pieces together. Our TextNormalizer class takes as input a language that is used to load the correct stopwords from the NLTK corpus. We could also customize the TextNormalizer to allow uses to choose between stemming and lemmatization, and pass the language into the SnowballStemmer. For filtering extraneous tokens, we create two methods. The first, is_punct(), checks if every character in the token has a Unicode category that starts with 'P' (for punctuation); the second, is_stopword() determines if the token is in our set of stopwords.

import unicodedata
from sklearn.base import BaseEstimator, TransformerMixin

class TextNormalizer(BaseEstimator, TransformerMixin):

    def __init__(self, language='english'):
        self.stopwords  = set(nltk.corpus.stopwords.words(language))
        self.lemmatizer = WordNetLemmatizer()

    def is_punct(self, token):
        return all(
            unicodedata.category(char).startswith('P') for char in token
        )

    def is_stopword(self, token):
        return token.lower() in self.stopwords

We can then add a normalize() method that takes a single document composed of a list of paragraphs, which are lists of sentences, which are lists of (token, tag) tuples—the data format that we preprocessed raw HTML to in Chapter 3.

    def normalize(self, document):
        return [
            self.lemmatize(token, tag).lower()
            for paragraph in document
            for sentence in paragraph
            for (token, tag) in sentence
            if not self.is_punct(token) and not self.is_stopword(token)
        ]

This method applies the filtering functions to remove unwanted tokens and then lemmatizes them. The lemmatize() method first converts the Penn Treebank part-of-speech tags that are the default tag set in the nltk.pos_tag function to WordNet tags, selecting nouns by default.

    def lemmatize(self, token, pos_tag):
        tag = {
            'N': wn.NOUN,
            'V': wn.VERB,
            'R': wn.ADV,
            'J': wn.ADJ
        }.get(pos_tag[0], wn.NOUN)

        return self.lemmatizer.lemmatize(token, tag)

Finally, we must add the Transformer interface, allowing us to add this class to a Scikit-Learn pipeline, which we’ll explore in the next section:

    def fit(self, X, y=None):
        return self

    def transform(self, documents):
        for document in documents:
            yield self.normalize(document)

Note that text normalization is only one methodology, and also utilizes NLTK very heavily, which may add unnecessary overhead to your application. Other options could include removing tokens that appear above or below a particular count threshold or removing stopwords and then only selecting the first five to ten thousand most common words. Yet another option is simply computing the cumulative frequency and only selecting words that contain 10%–50% of the cumulative frequency distribution. These methods would allow us to ignore both the very low frequency hapaxes (terms that appear only once) and the most common words, enabling us to identify the most potentially predictive terms in the corpus.

Caution

The act of text normalization should be optional and applied carefully because the operation is destructive in that it removes information. Case, punctuation, stopwords, and varying word constructions are all critical to understanding language. Some models may require indicators such as case. For example, a named entity recognition classifier, because in English, proper nouns are capitalized.

An alternative approach is to perform dimensionality reduction with Principal Component Analysis (PCA) or Singular Value Decomposition (SVD), to reduce the feature space to a specific dimensionality (e.g., five or ten thousand dimensions) based on word frequency. These transformers would have to be applied following a vectorizer transformer, and would have the effect of merging together words that are similar into the same vector space.

Pipelines

The machine learning process often combines a series of transformers on raw data, transforming the dataset each step of the way until it is passed to the fit method of a final estimator. But if we don’t vectorize our documents in the same exact manner, we will end up with wrong or, at the very least, unintelligible results. The Scikit-Learn Pipeline object is the solution to this dilemma.

Pipeline objects enable us to integrate a series of transformers that combine normalization, vectorization, and feature analysis into a single, well-defined mechanism. As shown in Figure 4-6, Pipeline objects move data from a loader (an object that will wrap our CorpusReader from Chapter 2) into feature extraction mechanisms to finally an estimator object that implements our predictive models. Pipelines are directed acyclic graphs (DAGs) that can be simple linear chains of transformers to arbitrarily complex branching and joining paths.

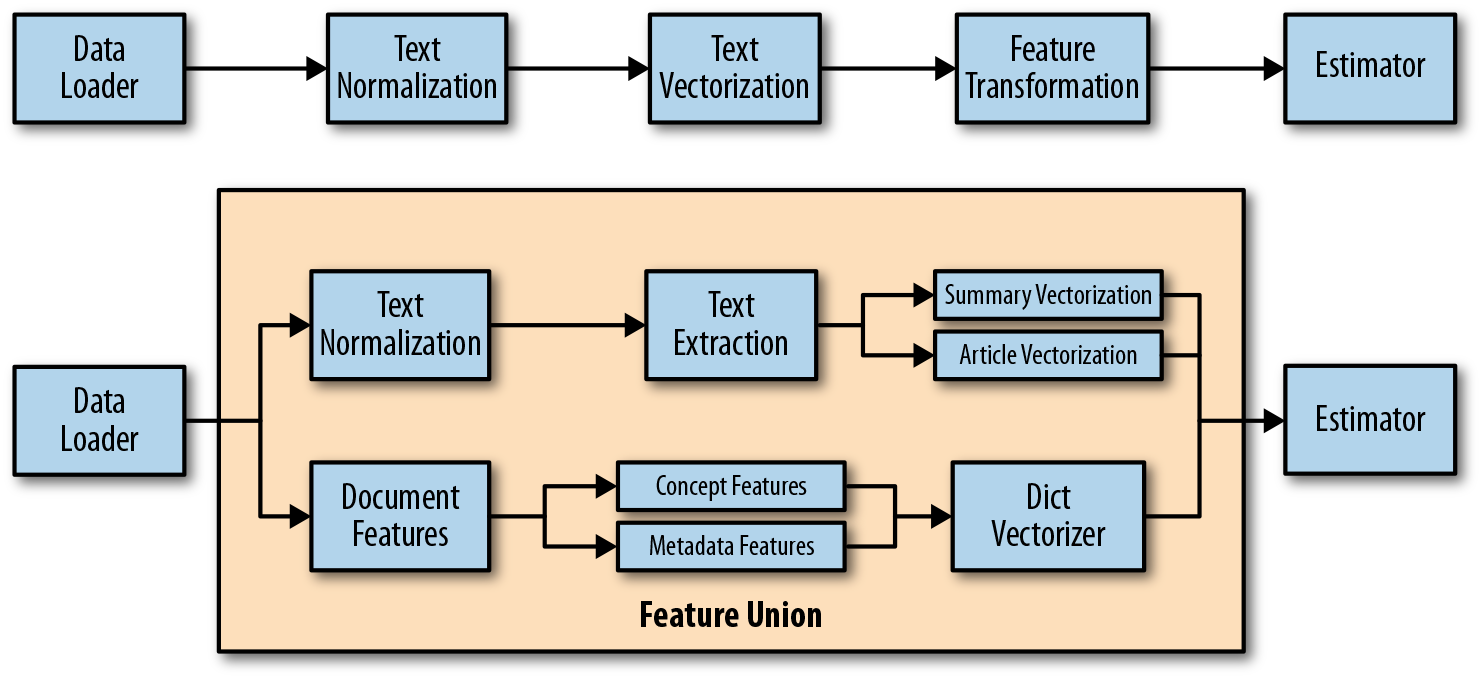
Figure 4-6. Pipelines for text vectorization and feature extraction

Pipeline Basics

The purpose of a Pipeline is to chain together multiple estimators representing a fixed sequence of steps into a single unit. All estimators in the pipeline, except the last one, must be transformers—that is, implement the transform method, while the last estimator can be of any type, including predictive estimators. Pipelines provide convenience; fit and transform can be called for single inputs across multiple objects at once. Pipelines also provide a single interface for grid search of multiple estimators at once. Most importantly, pipelines provide operationalization of text models by coupling a vectorization methodology with a predictive model.

Pipelines are constructed by describing a list of (key, value) pairs where the key is a string that names the step and the value is the estimator object. Pipelines can be created either by using the make_pipeline helper function, which automatically determines the names of the steps, or by specifying them directly. Generally, it is better to specify the steps directly to provide good user documentation, whereas make_pipeline is used more often for automatic pipeline construction.

Pipeline objects are a Scikit-Learn specific utility, but they are also the critical integration point with NLTK and Gensim. Here is an example that joins the TextNormalizer and GensimVectorizer we created in the last section together in advance of a Bayesian model. By using the Transformer API as discussed earlier in the chapter, we can use TextNormalizer to wrap NLTK CorpusReader objects and perform preprocessing and linguistic feature extraction. Our GensimVectorizer is responsible for vectorization, and Scikit-Learn is responsible for the integration via Pipelines, utilities like cross-validation, and the many models we will use, from Naive Bayes to Logistic Regression.

from sklearn.pipeline import Pipeline
from sklearn.naive_bayes import MultinomialNB

model = Pipeline([
    ('normalizer', TextNormalizer()),
    ('vectorizer', GensimVectorizer()),
    ('bayes', MultinomialNB()),
])

The Pipeline can then be used as a single instance of a complete model. Calling model.fit is the same as calling fit on each estimator in sequence, transforming the input and passing it on to the next step. Other methods like fit_transform behave similarly. The pipeline will also have all the methods the last estimator in the pipeline has. If the last estimator is a transformer, so too is the pipeline. If the last estimator is a classifier, as in the example above, then the pipeline will also have predict and score methods so that the entire model can be used as a classifier.

The estimators in the pipeline are stored as a list, and can be accessed by index. For example, model.steps[1] returns the tuple ('vectorizer', GensimVectorizer​(path=None)). However, common usage is to identify estimators by their names using the named_steps dictionary property of the Pipeline object. The easiest way to access the predictive model is to use model.named_steps["bayes"] and fetch the estimator directly.

Grid Search for Hyperparameter Optimization

In Chapter 5, we will talk more about model tuning and iteration, but for now we’ll simply introduce an extension of the Pipeline, GridSearch, which is useful for hyperparameter optimization. Grid search can be implemented to modify the parameters of all estimators in the Pipeline as though it were a single object. In order to access the attributes of estimators, you would use the set_params or get_params pipeline methods with a dunderscore representation of the estimator and parameter names as follows: estimator__parameter.

Let’s say that we want to one-hot encode only the terms that appear at least three times in the corpus; we could modify the Binarizer as follows:

model.set_params(onehot__threshold=3.0)

Using this principle, we could execute a grid search by defining the search parameters grid using the dunderscore parameter syntax. Consider the following grid search to determine the best one-hot encoded Bayesian text classification model:

from sklearn.model_selection import GridSearchCV

search = GridSearchCV(model, param_grid={
    'count__analyzer': ['word', 'char', 'char_wb'],
    'count__ngram_range': [(1,1), (1,2), (1,3), (1,4), (1,5), (2,3)],
    'onehot__threshold': [0.0, 1.0, 2.0, 3.0],
    'bayes__alpha': [0.0, 1.0],
})

The search nominates three possibilities for the CountVectorizer analyzer parameter (creating n-grams on word boundaries, character boundaries, or only on characters that are between word boundaries), and several possibilities for the n-gram ranges to tokenize against. We also specify the threshold for binarization, meaning that the n-gram has to appear a certain number of times before it’s included in the model. Finally the search specifies two smoothing parameters (the bayes_alpha parameter): either no smoothing (add 0.0) or Laplacian smoothing (add 1.0).

The grid search will instantiate a pipeline of our model for each combination of features, then use cross-validation to score the model and select the best combination of features (in this case, the combination that maximizes the F1 score).

Enriching Feature Extraction with Feature Unions

Pipelines do not have to be simple linear sequences of steps; in fact, they can be arbitrarily complex through the implementation of feature unions. The FeatureUnion object combines several transformer objects into a new, single transformer similar to the Pipline object. However, instead of fitting and transforming data in sequence through each transformer, they are instead evaluated independently and the results are concatenated into a composite vector.

Consider the example shown in Figure 4-7. We might imagine an HTML parser transformer that uses BeautifulSoup or an XML library to parse the HTML and return the body of each document. We then perform a feature engineering step, where entities and keyphrases are each extracted from the documents and the results passed into the feature union. Using frequency encoding on the entities is more sensible since they are relatively small, but TF–IDF makes more sense for the keyphrases. The feature union then concatenates the two resulting vectors such that our decision space ahead of the logistic regression separates word dimensions in the title from word dimensions in the body.

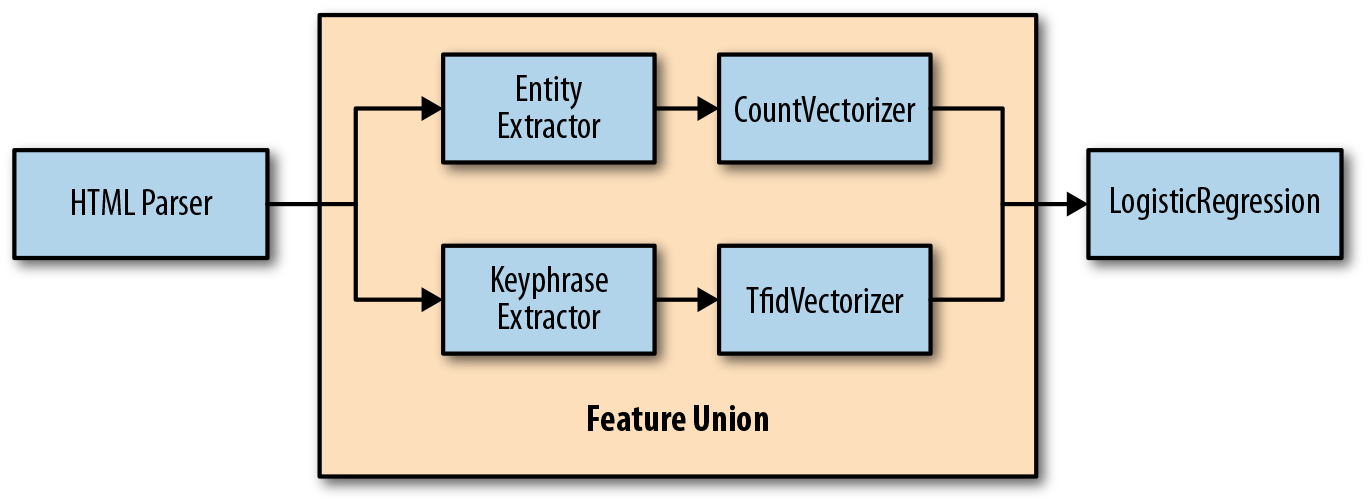
Figure 4-7. Feature unions for branching vectorization

FeatureUnion objects are similarly instantiated as Pipeline objects with a list of (key, value) pairs where the key is the name of the transformer, and the value is the transformer object. There is also a make_union helper function that can automatically determine names and is used in a similar fashion to the make_pipeline helper function—for automatic or generated pipelines. Estimator parameters can also be accessed in the same fashion, and to implement a search on a feature union, simply nest the dunderscore for each transformer in the feature union.

Given the unimplemented EntityExtractor and KeyphraseExtractor transformers mentioned above, we can construct our pipeline as follows:

from sklearn.pipeline import FeatureUnion
from sklearn.linear_model import LogisticRegression

model = Pipeline([
    ('parser', HTMLParser()),
    ('text_union', FeatureUnion(
        transformer_list = [
            ('entity_feature', Pipeline([
                ('entity_extractor', EntityExtractor()),
                ('entity_vect', CountVectorizer()),
            ])),
            ('keyphrase_feature', Pipeline([
                ('keyphrase_extractor', KeyphraseExtractor()),
                ('keyphrase_vect', TfidfVectorizer()),
            ])),
        ],
        transformer_weights= {
            'entity_feature': 0.6,
            'keyphrase_feature': 0.2,
        }
    )),
    ('clf', LogisticRegression()),
])

Note that the HTMLParser, EntityExtractor and KeyphraseExtractor objects are currently unimplemented but are used for illustration. The feature union is fit in sequence with respect to the rest of the pipeline, but each transformer within the feature union is fit independently, meaning that each transformer sees the same data as the input to the feature union. During transformation, each transformer is applied in parallel and the vectors that they output are concatenated together into a single larger vector, which can be optionally weighted, as shown in Figure 4-8.

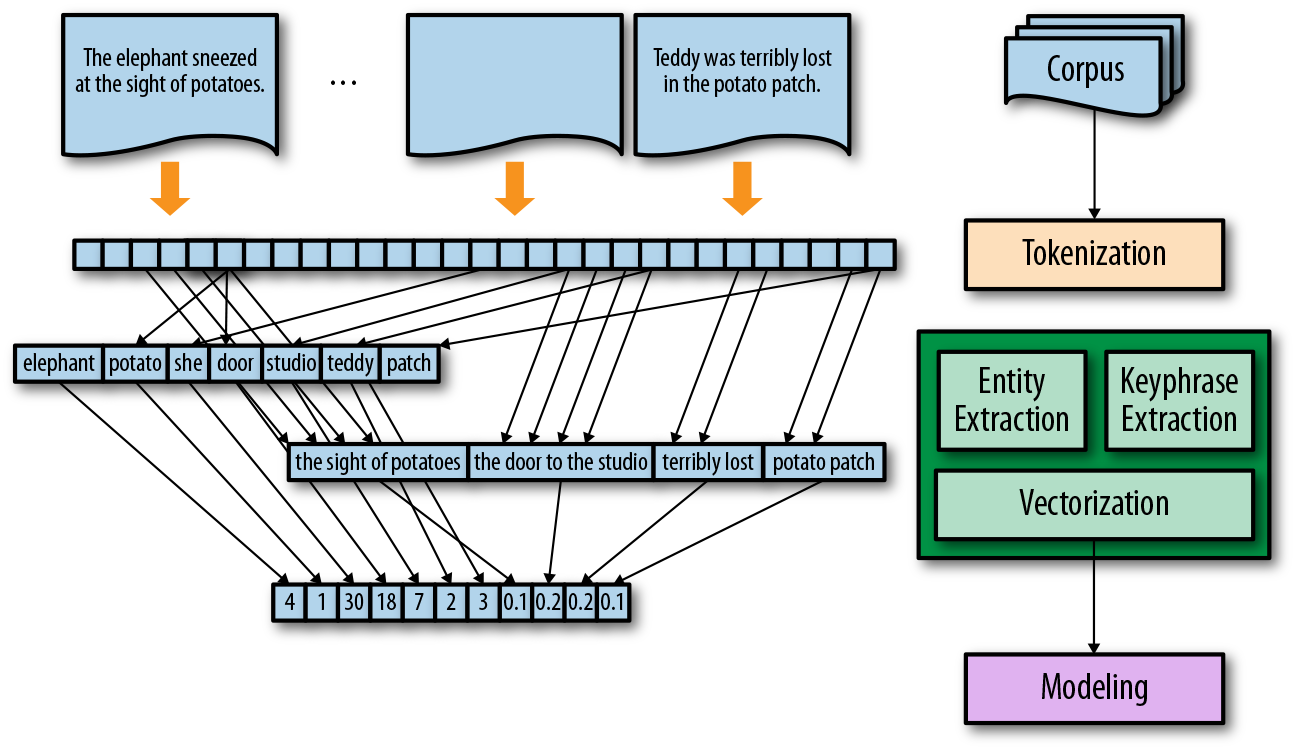
Figure 4-8. Feature extraction and union

In this example, we are weighting the entity_feature transformer more than the keyphrase_feature transformer. Using combinations of custom transformers, feature unions, and pipelines, it is possible to define incredibly rich feature extraction and transformation in a repeatable fashion. By collecting our methodology into a single sequence, we can repeatably apply the transformations, particularly on new documents when we want to make predictions in a production environment.

Conclusion

In this chapter, we conducted a whirlwind overview of vectorization techniques and began to consider their use cases for different kinds of data and different machine learning algorithms. In practice, it is best to select an encoding scheme based on the problem at hand; certain methods substantially outperform others for certain tasks.

For example, for recurrent neural network models it is often better to use one-hot encoding, but to divide the text space one might create a combined vector for the document summary, document header, body, etc. Frequency encoding should be normalized, but different types of frequency encoding can benefit probabilistic methods like Bayesian models. TF–IDF is an excellent general-purpose encoding and is often used first in modeling, but can also cover a lot of sins. Distributed representations are the new hotness, but are performance intensive and difficult to scale.

Bag-of-words models have a very high dimensionality, meaning the space is extremely sparse, leading to difficulty generalizing the data space. Word order, grammar, and other structural features are natively lost, and it is difficult to add knowledge (e.g., lexical resources, ontological encodings) to the learning process. Local encodings (e.g., nondistributed representations) require a lot of samples, which could lead to overtraining or underfitting, but distributed representations are complex and add a layer of “representational mysticism.”

Ultimately, much of the work for language-aware applications comes from domain-specific feature analysis, not just simple vectorization. In the final section of this chapter we explored the use of FeatureUnion and Pipeline objects to create meaningful extraction methodologies by combining transformers. As we move forward, the practice of building pipelines of transformers and estimators will continue to be our primary mechanism of performing machine learning. In Chapter 5 we will explore classification models and applications, then in Chapter 6 we will take a look at clustering models, often called topic modeling in text analysis. In Chapter 7, we will explore some more complex methods for feature analysis and feature exploration that will assist in finetuning our vector-based models to achieve better results. Nonetheless, simple models that only consider word frequencies are often very successful. In our experience, a pure bag-of-words model works about 85% of the time!

¹ Quoc V. Le and Tomas Mikolov, Distributed Representations of Sentences and Documents, (2014) http://bit.ly/2GJBHjZ