Arithmetic and Logic in Computer Systems

6

Sequential Division

Unlike addition, subtraction and multiplication, division does not, in general, produce an exact answer, because the dividend is not necessarily a multiples of the divisor. A variety of division algorithms are to be described in the rest of this chapter.

6.1 SUBTRACT-AND-SHIFT APPROACH

Let's look at an example of pencil-and-paper division in Figure 6.1.

Here 2746 is referred to as the Dividend, 32 is the Divisor, 85 the Quotient and 26 the Remainder. After 274 – 256 is performed in the first step, 18 is obtained as a partial remainder. By pulling down 6, 18 becomes 180 (+6). On digital computers, most of the division operations are performed in a recursive procedure represented by the following formula:

where j = 0, 1, · · ·, n − 1 is the recursion index, R^(j) is the partial remainder in the jth iteration. The initial partial remainder R⁽⁰⁾ equals the dividend, and R⁽ⁿ⁾ is the final remainder. The quotient is determined digit by digit in the recursive procedure, with q_j+1 being the (j + 1)th quotient digit. D is the divisor, and r is the radix. In the above example r = 10.

From the recursion formula, we have

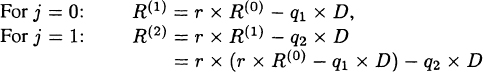
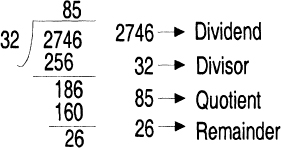
Fig. 6.1: Pencil-and-Paper Division

Let's look at ...