Audio Signal Processing and Coding

3.6 ENTROPY CODING

It is worthwhile to consider the theoretical limits for the minimum number of bits required to represent an audio sample. Shannon, in his mathematical theory of communication [Shan48], proved that the minimum number of bits required to encode a message, X, is given by the entropy, H_e(X). The entropy of an input signal can be defined as follows. Let X = [x₁, x₂, … , x_N] be the input data vector of length N and p_i be the probability that i-th symbol (over the symbol set, V = [υ₁, υ₂, … , υ_K]) is transmitted. The entropy, H_e(X), is given by

In simple terms, entropy is a measure of uncertainty of a random variable. For example, let the input bitstream to be encoded be X = [4 5 6 6 2 5 4 4 5 4 4], i.e., N = 11; symbol set, V = [2 4 5 6] and the corresponding probabilities are , respectively, with K = 4. The entropy, H_e(X), can be computed as follows:

Table 3.3. An example entropy code for Example 3.2.

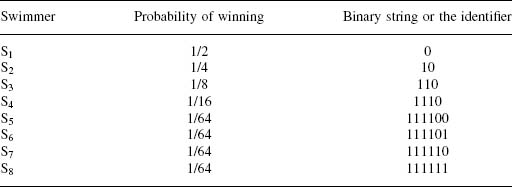
Example 3.2

Consider eight swimmers {S₁, S₂, S₃, S₄, S₅, S₆, S₇, and S₈} in a race with win probabilities {1/2, 1/4, 1/8, 1/16, 1/64, 1/64, 1/64, and 1/64}, respectively. ...