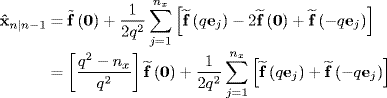8.2 Multidimensional Finite Difference Kalman Filters
8.2.1 Multidimensional Finite Difference State Prediction
In manner similar to the approach taken in the one-dimensional case, we first repeat the multidimensional state prediction equation developed for the EKF given by (7.33)
Now, using the second-order finite difference term of multidimensional Stirling's polynomial given by equation (2.74) and letting x → c and x0 = 0, (8.26) becomes
where ej is a unit vector along the Cartesian axis of the j th dimension and q is a step size that must be finite, real, and greater than zero.
Defining
leads to the identities
(8.29) ![]()
and
(8.30) ![]()
Here, ![]() is a free parameter that determines the value of q. To maintain q as finite, real, and greater than zero, we must restrict
is a free parameter that determines the value of q. To maintain q as finite, real, and greater than zero, we must restrict ![]() to the ...
to the ...
Get Bayesian Estimation and Tracking: A Practical Guide now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.