Big Java, 4th Edition

Appendix I. Number Systems

Binary Numbers

Decimal notation represents numbers as powers of 10, for example

There is no particular reason for the choice of 10, except that several historical number systems were derived from people's counting with their fingers. Other number systems, using a base of 12, 20, or 60, have been used by various cultures throughout human history. However, computers use a number system with base 2 because it is far easier to build electronic components that work with two values, which can be represented by a current being either off or on, than it would be to represent 10 different values of electrical signals. A number written in base 2 is also called a binary number.

For example,

For digits after the "decimal" point, use negative powers of 2.

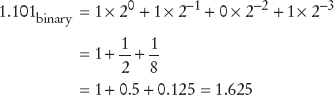
In general, to convert a binary number into its decimal equivalent, simply evaluate the powers of 2 corresponding to digits with value 1, and add them up. Table 1 shows the first powers of 2.

To convert a decimal integer into its binary equivalent, keep dividing the integer by 2, keeping track of the remainders. Stop when the number is 0. Then write the remainders as a binary number, starting with the last one.

For example,

Therefore, ...