6 Brownian motion as a Markov process
We have seen in 2.13 that for a d-dimensional Brownian motion (Bt)t≥0 and any s > 0 the shifted process Wt := Bt+s - Bs, t ≥ 0, is again a BMd which is independent of (Bt)0≤t≤s. Since Bt+s = Wt + Bs, we can interpret this as a renewal property: Rather than going from 0 = B0 straight away to x = Bt+s in (t + s) units of time, we stop after time s at x′ = Bs and move, using a further Brownian motion Wt for t units of time, from x’ to x = Bt+s. This situation is shown in Figure 6.1:
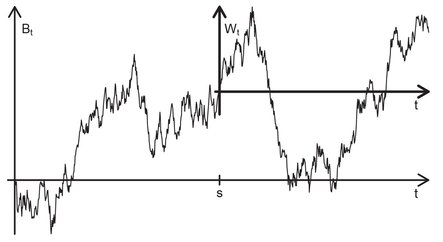
Fig. 6.1. Wt := Bt+s - Bs, t ≥ 0, is a Brownian motion in the new coordinate system with origin (s, Bs).
6.1 The Markov property ...
Get Brownian Motion, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

