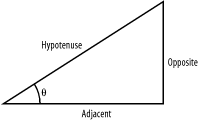
You need to calculate the length of one side of a triangle when either the lengths of two sides are known or one angle and the length of a side are known.
Use the Math.Sin,
Math.Cos, and Math.Tan methods
of the Math class to find the length of one side.
The equations for these methods are as follows:
double theta = 40; double hypotenuse = 5; double oppositeSide; double adjacentSide; oppositeSide = Math.Sin(theta) * hypotenuse; oppositeSide = Math.Tan(theta) * adjacentSide; adjacentSide = Math.Cos(theta) * hypotenuse; adjacentSide = oppositeSide / Math.Tan(theta); hypotenuse = oppositeSide / Math.Sin(theta); hypotenuse = adjacentSide / Math.Cos(theta);
where theta (Θ) is the known angle, and the oppositeSide variable
is equal to the length of the side opposite to
the angle theta, and the
adjacentSide variable is equal to the length of
the side adjacent to the angle
theta. The hypotenuse variable
is equal to the length of the hypotenuse of the
triangle. See Figure 1-1.
In addition to these three static methods, the length of the
hypotenuse of a right triangle can be calculated using the
Pythagorean theorem. This theorem states
that the hypotenuse of a right triangle is equal to the square root
of the sum of the squares of the other two sides.
This
equation can be realized through the use of the
Math.Pow and Math.Sqrt static
methods of the Math class, as follows:
double hypotenuse = Math.Sqrt(Math.Pow(xSide, 2) + Math.Pow(ySide, 2))
where xSide and ySide are the
lengths of the two sides that are not the
hypotenuse of the triangle.
Finding the length of a side of a right triangle is easy when an angle and the length of one of the sides are known. Using the trigonometric functions sine, cosine, and tangent, we can derive the lengths of either of the two unknown sides. The equations for sine, cosine, and tangent are defined here:
sin(Theta) = oppositeSide / hypotenuseSide cos(Theta) = adjacentSide / hypotenuseSide tan(Theta) = oppositeSide / adjacentSide
where theta is the value of the known angle.
Rearranging these equations allows us to derive the following
equations:
oppositeSide = sin(theta) * hypotenuse; oppositeSide = tan(theta) * adjacentSide; adjacentSide = cos(theta) * hypotenuse; adjacentSide = oppositeSide / tan(theta); hypotenuse = oppositeSide / sin(theta); hypotenuse = adjacentSide / cos(theta);
These equations give us two methods to find the length of each side of the triangle.
In the case where none of the angles are known, but the lengths of two of the sides are known, use the Pythagorean theorem to determine the length of the hypotenuse. This theorem is defined as follows:
Math.Sqrt(Math.Pow(hypotenuse)) = Math.Sqrt(Math.Pow(xSide, 2) + Math.Pow(ySide, 2))
Simplifying this equation into a syntax usable by C#, we obtain the following code:
double hypotenuse = Math.Sqrt(Math.Pow(xSide, 2) + Math.Pow(ySide, 2));
where hypotenuse is equal to the length of the
hypotenuse, and xSide and ySide
are the lengths of the other two sides.
Get C# Cookbook now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.