Computer Security and Cryptography

11.6 CRYPTANALYSIS OF THE MERKLE–HELLMAN KNAPSACK SYSTEM (MODULAR MAPPING) [SHAMIR, 1982]

UCSB has been the site of a meeting dealing with current topics in cryptography starting with CRYPTO ’81 in 1981. Adi Shamir electrified the attendees at CRYFTO ’82 by presenting an analysis of the Merkle–Hellman cryptosystem. A program running on an Apple during his lecture illustrated the solution technique that we now describe.

The mapping T_ω⁻¹,_m: s = (s₀, s₁, …, s_n−1) → a = (a₀, a₁, …, a_n−1) from the super-increasing to the public knapsack vector is nonlinear and this was the basis for believing that the Merkle–Hellman scheme provided a secure public-key encipherment scheme.

For define the modular mapping (function) ϕ_a,m(w) for 0 ≤ a, w < m (Fig. 11.1) by

• The continuous representation of the discrete-valued function ϕ_a,m(w) consists of straight-line segments with slope
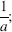
• ϕ_{a, m} (w) has minima nearly equal to 0 at the points 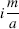with i = 0, 1, …, a − 1; the distance between consecutive minima is larger than 1.

Write

Figure 11.1 The modular mapping function.

where k_j is an integer <m. According ...