Computer Security and Cryptography

3.5 PRUNING FROM THE TABLE OF ISOMORPHS

We identify the repeated trials of the experiment ∈ with the generation of plaintext with letters in the generic alphabet by the iid language model with probabilities π(i) = Pr{X = i} for 0 ≤ i < m.

To test if the ciphertext r-gram v is an isomorph of the plaintext u, the ciphertext letter counts {N_vi} are compared to the plaintext letter probabilities using the χ²-statistic:

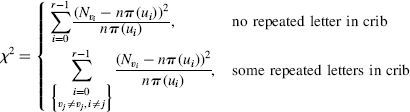
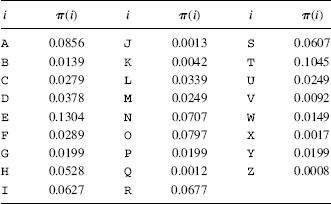
Table 3.5 lists the count of 1-grams {N_i} and their frequencies f(i) = N_i/n in the ciphertext cipherEx3.1. Table 3.6 gives the probabilities {π(i)} of 1-grams derived from a large sample English language text. The plan is to now use the χ²-test to associate the seven high-frequency ciphertext letters in Table 3.5:

TABLE 3.5 Letter Counts and Frequencies in cipherEx3.1

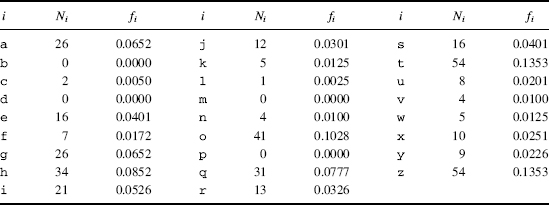
TABLE 3.6 1-Gram English-Language Plaintext Probabilities

with seven of the nine plaintext letters of highest probability from Table 3.6:

A correspondence between t, z, o, h and some subset of E, T, A, O, N, ...