Computer Security and Cryptography

3.9 GAUSSIAN ELIMINATION

Let A = (a_i,j be an n × n matrix and x = (x₁, x₂,…, x_n), y = (y₁, y₂,…, y_n) be n-vectors, all with real number entries satisfying

If det(A) ≠ 0, then for every y, the linear system of Equations (3.20) has a unique solution x,

Gaussian elimination is a process in which transformations are applied to an invertible matrix A to produce the identity matrix I and thereby obtain the solution for x in Equation (3.20).

3.9.1 Elementary Row and Column Matrix Transformations

1. R_r,s(v) (r ≠ s) is the n × n matrix equal to the identity matrix, except that the element in position (r, s) of R_r,s(v) is v. For example when n = 4

   

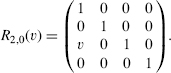
   If

   

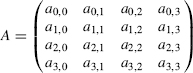
   then

   

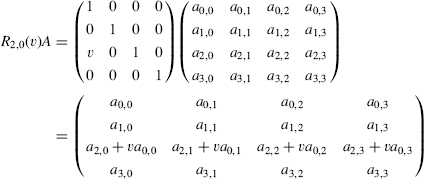
   Premultiplication of A by R_{r, s}(v) replaces the rth row of A by the sum of

   • v times the sth row of A and
   • The rth row of A.

     The inverse of R_{r, s}(v) is R_{r, s}(− v).

2. C_{r, s}(v) (r ≠ s) is the n × n matrix, which is equal to the identity matrix except that the element in position (r, s) of C_r,s(v) is v. For example, when n = 4

   If

   then

   Postmultiplication ...