Designing Embedded Hardware, 2nd Edition

RC Circuits

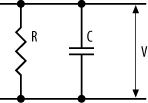
Combining resistors and capacitors can yield some interesting and useful effects. A resistor-capacitor combination is known as an RC circuit, and it can take one of three forms. The first form is where the resistor and capacitor are in parallel (Figure 4-31).

Figure 4-31. Resistor and capacitor in parallel

Now, what does this do? A voltage (V) applied across the pair will charge the capacitor (as well as some current flowing down through the resistor). When the applied voltage is removed, the capacitor will discharge through the resistor. The resistor will limit the rate of discharge, since it limits current flow. From Ohm's Law, we have:

   I = - V / R

(The negative voltage is because we're discharging the capacitor.) Now, the current flow out of a capacitor is given by:

   I = C * dV/dt

So, we have:

   dV/dt = - V / RC

Integrating this with respect to time, with zero initial conditions, gives us:

   V = e-t/RC

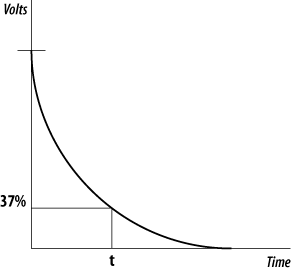
This gives us the discharge waveform shown in Figure 4-32, which represents the voltage across the capacitor.

A parallel RC circuit will provide an exponential decay in the output voltage. The value for t when the output voltage is at 37% of the maximum is known as the time constant for the circuit and is simply the product of R and C:

   t = R * C

For example, a parallel RC circuit where the resistor is 100 kΩ and the capacitor is 10 uF gives a time constant of 1 second.

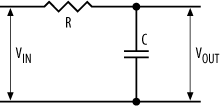
The second form of RC circuit is the series RC circuit, shown in Figure 4-33.

When a voltage is applied at the input to the RC circuit (on the left), current will flow through the resistor and the capacitor will begin to charge. However, the resistor limits current flow and therefore will limit the rate at which the capacitor charges.

Figure 4-32. Discharge of a parallel RC circuit

Figure 4-33. Series RC circuit

Now, the current flowing into the capacitor is again given by the relation:

   I = C * dV/dt

This current is the same as that which is flowing through the resistor, and by Ohm's Law, we have that this current is given by:

   I = (VIN - VOUT) / R

where V_IN - V_OUT is the voltage drop across the resistor. Combining these two equations gives us the differential equation:

   dV / dt = (VIN - VOUT) / RC

Integrating this gives us the voltage at the capacitor as:

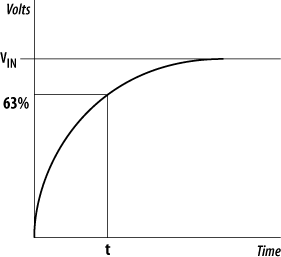
   VOUT = VIN (1 - e-t/RC)

Again, this is an exponential equation; however, this time it represents an exponential charging of the capacitor. The waveform for the voltage at the capacitor is shown in Figure 4-34.

In this case, the time constant is the time for the voltage at the capacitor to reach 63% (total - 37%) of the input voltage. As before, this time constant is simply the product of R and C.

Figure 4-34. Charging of a series RC circuit

This form of RC circuit is a simple type of low-pass filter . This is a circuit that provides a path to ground for high-frequency components of a signal, thereby attenuating them from the main signal, while the low-frequency components suffer far less attenuation. This type of circuit is very useful for removing high-frequency noise that may be superimposed on a signal.

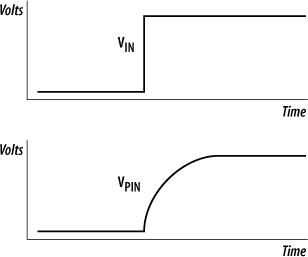
A given processor or peripheral chip will have a small amount of input capacitance on each input pin. This, combined with the small inherent impedance of a circuit connection and the input impedance of the pin, means that an applied digital voltage to the pin will actually appear as an exponential rise, rather than as a sharp (digital) edge (Figure 4-35). These effects are minimal but can be significant in high-speed circuits or where several devices are connected to the same signal line and the overall input capacitance is not insignificant.

Figure 4-35. RC charging at a chip's input pin

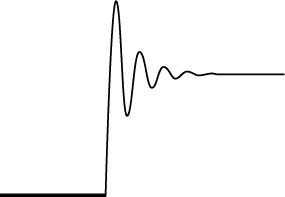
The effect of lead inductance can contribute second-order characteristics, such as those shown in Figure 4-36. These inductive effects create "ringing" when a sudden voltage change is applied. Inductors will be discussed shortly.

Figure 4-36. Inductive effects cause ringing on a signal input

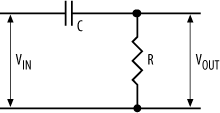
The third form of an RC circuit is shown in Figure 4-37.

Figure 4-37. RC filter

This type of circuit is a simple form of a high-pass filter , since it passes only the high frequencies through to the output. The capacitor in such a circuit is known as a blocking capacitor.