Digital Signal Processing Techniques and Applications in Radar Image Processing

1

SIGNAL THEORY AND ANALYSIS

A signal, in general, refers to an electrical waveform whose amplitude varies with time. Signals can be fully described in either the time or frequency domain. This chapter discusses the characteristics of signals and identifies the main tools used for signal processing. Some functions widely used in signal processing are described in Section 1.1. A quick review of the linear system and convolution theory is covered in Section 1.2. Fourier series representation of periodic signals is discussed in Section 1.3. Fourier transform of nonperiodic signals and periodic signals are covered in Sections 1.4 and 1.5, respectively. Section 1.6 describes sampling theory together with signal interpolation. Some advanced sampling and interpolation techniques are reviewed in Section 1.7.

1.1 SPECIAL FUNCTIONS USED IN SIGNAL PROCESSING

1.1.1 Delta or Impulse Function δ(t)

The delta function or impulse function δ(t) is defined as

and

On the basis of this definition, one can obtain

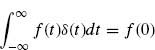
and

1.1.2 Sampling or Interpolation Function sinc (t)

The function sinc (t) is defined as