Equity Hybrid Derivatives

CHAPTER 3

Short-Rate Models

3.1 INTRODUCTION

When pricing equity derivatives, we generally need to model only a single market instrument: the stock price.¹ The interest rate world, on the other hand, consists of many instruments: futures, swaps, and the like, all of which can move independently. These are generally combined to form the yield curve, commonly expressed in terms of zero coupon bond prices P(t, T) (i.e., the value seen at time t of 1 unit of currency paid at time T) or the zero coupon rate R(t, T), defined by

Another useful representation is in terms of the forward rate, f(t, T). This is defined as the rate, fixed at time t, for instantaneous borrowing at time T. If we agree at time t that we will invest 1 at time T for an infinitesimal period δ, the amount we will get back at time T + δ is 1 + f(t, T)δ. We can hedge this by shorting the zero coupon bond with maturity T and buying 1 + f(t, T)δ units of the zero coupon bond with maturity T + δ, making

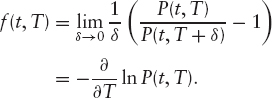
The EUR yield curve is shown in terms of R(0, T) and f(0, T) in figure 3.1.

Two different approaches to interest rate modeling are

• Market models, where we model the market instruments such as LIBOR² or CMS³ rates directly. Examples of market models include the well-known BGM model [59].

  FIGURE 3.1 EUR yield curve in terms ...