Equity Hybrid Derivatives

CHAPTER 8

Forward PDEs and Local Volatility Calibration

8.1 INTRODUCTION

8.1.1 Local and Implied Volatilities

In the Black-Scholes model ([134]), the stock price follows geometric Brownian motion with a constant volatility σ:

where r_t is the short interest rate and ν_t contains the repo rate and a dividend yield. This is discussed in more detail in chapter 1. Under this assumption, the price of a European call option with strike K and maturity T is given by the Black-Scholes formula

where P(t, T) is the price at time t of a zero-coupon bond with maturity T, F_T is the stock forward, and

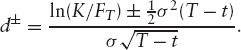
Now that the European options themselves form a liquid market, prices are available for many options on many stocks and indices. The implied volatility of an option is the constant volatility that when used in the above equations recovers the market price of the option. Figure 8.1 shows the dependence of the implied volatility of the Stoxx50 index on the maturity and strike of the options.

Since the implied volatility is a function of the strike price, the volatility that we use in equation (8.1) cannot be constant. If we want our stock model to be Markovian in just one factor, we must make the volatility ...