PART III: PROBLEMS
Section 2.2
2.2.1 Consider the binomial distribution with parameters n, θ, 0 < θ < 1.
Write an algorithm for the computation of b(j | n, θ) employing the recursive relationship
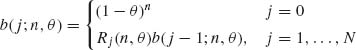
where Rj (n, θ) = b(j;n, θ)/b(j – 1; n, θ). Write the ratio Rj (n, θ) explicitly and find an expression for the mode of the distribution, i.e., ![]() = smallest nonnegative integer for which b(x0;n, θ) ≥ b(j; n, θ) for all j = 0, …, n.
= smallest nonnegative integer for which b(x0;n, θ) ≥ b(j; n, θ) for all j = 0, …, n.
2.2.2 Prove formula (2.2.2).
2.2.3 Determine the median of the binomial distribution with n = 15 and θ = .75.
2.2.4 Prove that when n → ∞, θ → 0, but nθ → λ, 0 < λ < ∞, then
![]()
where p(i; λ) is the p.d.f. of the Poisson distribution.
2.2.5 Establish formula (2.2.7).
2.2.6 Let X have the Pascal distribution with parameters ν (fixed positive integer) and θ, 0 < θ < 1. Employ the relationship between the Pascal distribution and the negative–binomial distribution to show that the median of X is ν + n.5, where n.5 = least nonnegative integer n such that Iθ (ν, n + 1) ≥ .5. [This formula of the median is useful for writing a computer program and utilizing the computer’s library subroutine function that computes Iθ (a, b).]
2.2.7 Apply formula (2.2.4) to prove the binomial ...
Get Examples and Problems in Mathematical Statistics now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

