Experiment!: Planning, Implementing and Interpreting

9.8 Working with Screening Designs

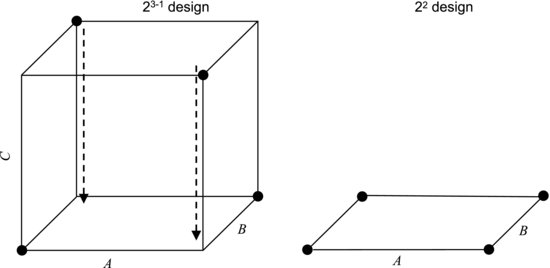
An interesting property of the half factorial design is that, if one factor turns out to be unimportant, the design collapses to a full factorial design. This is most easily understood looking at it graphically. The left part of Figure 9.8 shows a three-factor half factorial design. The dots in the corners show the treatments used and we see that every other treatment is missing from the corresponding full factorial design, which is represented by all the corners of the cube. If, for instance, factor C turns out not to have a significant effect on the response, this means that there is no discernible difference in the response when C is switched between its two levels. In other words, a change in the setting of C only measures the experimental error. This could be seen as the cube collapsing along the C-direction. As shown in the right-hand part of the figure, we then obtain a full factorial design with the remaining two factors A and B. If these factors turn out to be significant, we now have data for a more detailed study of them.

Figure 9.8 The three-factor half factorial design may collapse to a two-factor full factorial design if one factor (here C) turns out to be unimportant.

The fact that every other corner point is missing can be advantageous in other ways than just reducing the number of runs. In the corners, all factors are set to ...