Feature Engineering for Machine Learning

Chapter 7. Nonlinear Featurization via K-Means Model Stacking

PCA is very useful when the data lies in a linear subspace like a flat pancake. But what if the data forms a more complicated shape?¹ A flat plane (linear subspace) can be generalized to a manifold (nonlinear subspace), which can be thought of as a surface that gets stretched and rolled in various ways.²

If a linear subspace is a flat sheet of paper, then a rolled up sheet of paper is a simple example of a nonlinear manifold. Informally, this is called a Swiss roll (see Figure 7-1). Once rolled, a 2D plane occupies 3D space. Yet it is essentially still a 2D object. In other words, it has low intrinsic dimensionality, a concept we’ve already touched upon in “Intuition”. If we could somehow unroll the Swiss roll, we’d recover the 2D plane. This is the goal of nonlinear dimensionality reduction, which assumes that the manifold is simpler than the full dimension it occupies and attempts to unfold it.

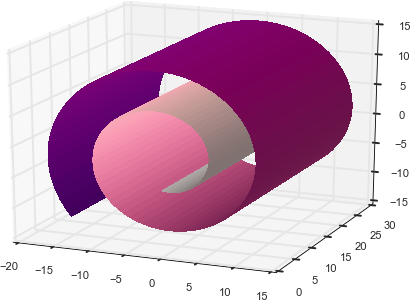
Figure 7-1. The Swiss roll, a nonlinear manifold

The key observation is that even when a big manifold looks complicated, the local neighborhood around each point can often be well approximated with a patch of flat surface. In other words, the patches to encode global structure using local structure.³ Nonlinear dimensionality reduction is also called nonlinear embedding or manifold learning. Nonlinear embeddings are useful for ...