3.11 Proofs for Section 2.6.3 “Asymptotic Results as N→ ∞ and Ts → 0′′
3.11.1 Proof of Lemma 2.6.12
Condition (2.209) holding uniformly w.r.t. τ assures that Assumption 2.6.11 is verified. The numbers Mp, possibly depending on 
, are independent of Ts. Under Assumption 2.6.11, the Weierstrass M-test (Johnsonbaugh and Pfaffenberger 2002, Theorem 62.6) assures the uniform convergence of the series of functions of Ts
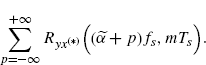
Therefore, the limit operation can be interchanged with the infinite sum
(3.207)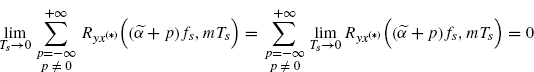 
where, in the second equality the sufficient condition (2.209) for Assumption 2.6.11 is used.
3.11.2 Proof of Theorem 2.6.13 Mean-Square Consistency of the Discrete-Time Cyclic Cross-Correlogram
From Lemma 2.6.12 we have
(3.208)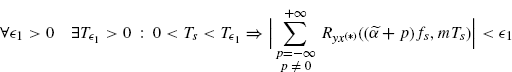 
(not necessarily uniformly with respect to 
and m).
From Theorems 2.6.4 and 2.6.5 it follows that, for every fixed Ts, 
, and m,
that is,
(3.210)
Therefore, for ...
Get Generalizations of Cyclostationary Signal Processing: Spectral Analysis and Applications now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
