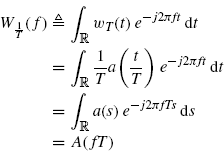Generalizations of Cyclostationary Signal Processing: Spectral Analysis and Applications

3.5 Proofs for Section 2.4.2 “Mean-Square Consistency of the Cyclic Cross-Correlogram”

In this section, proofs of results presented in Section 2.4.2 on the mean-square consistency of the cyclic cross-correlogram are reported.

Lemma 3.5.1 Let a(t) be such that Assumption 2.4.5 is satisfied. We have the following.

a. The Fourier transform

(3.60)

is bounded, continuous, and infinitesimal as |f|→ ∞.

b. We have the result

(3.61)

where δ_f denotes Kronecker delta, that is, δ_f = 1 if f = 0 and δ_f = 0 if f ≠ 0.

Proof: Since , item (a) is a consequence of the properties of the Fourier transforms (Champeney 1990). In Assumption 2.4.5 it is also assumed that there exists γ > 0 such that

(3.62)

In reference to item (b), observe that from (2.125) we have

(3.63)

where, in the third equality, the variable change s = t/T is made. Thus, for f = 0,

(3.64)

(see (2.126)). For f ≠ 0, since , we have ...