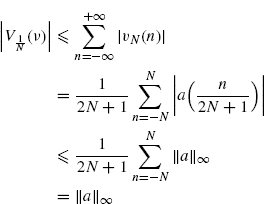Generalizations of Cyclostationary Signal Processing: Spectral Analysis and Applications

3.9 Proofs for Section 2.6.1 “Discrete-Time Cyclic Cross-Correlogram”

3.9.1 Proof of Theorem 2.6.2 Expected Value of the Discrete-Time Cyclic Cross-Correlogram

By taking the expected value of both sides in (2.181) and using (2.174c) we get

(3.143)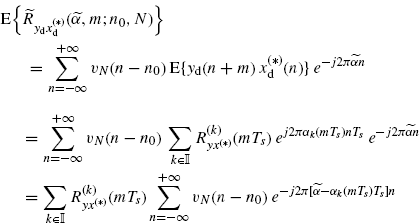

from which (2.183) immediately follows.

The data-tapering window is finite length (see (2.182)). Thus, in the first equality the sum over n is finite and can be freely interchanged with the expectation operator. In the second equality, Assumption 2.4.2a is used. In the third equality the order of the two sums can be interchanged since the double-index series over k and n is absolutely convergent (Johnsonbaugh and Pfaffenberger 2002, Theorem 29.4). In fact,

(3.144)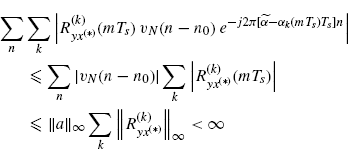

where Assumption 2.4.3a, (2.182), and the inequality (Assumption 2.4.5)

(3.145)

are used.

By substituting (2.182) into the first line of (2.184) we get

(3.146)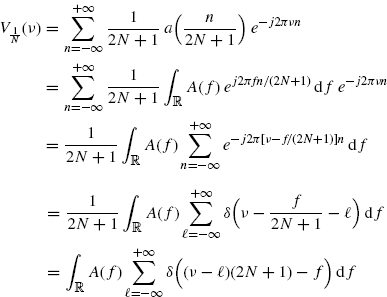

from which the right-hand side of (2.184) immediately follows. In (3.92), in the fourth equality the Poisson's sum formula ...