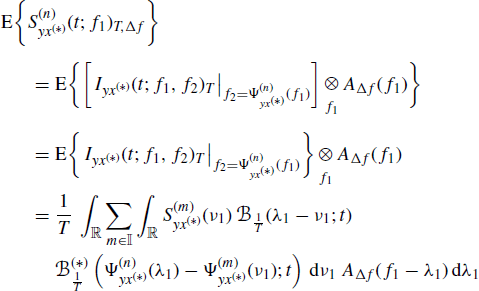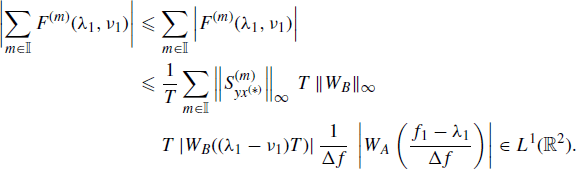Generalizations of Cyclostationary Signal Processing: Spectral Analysis and Applications

5.4 Proofs for Section 4.6 “The Frequency-Smoothed Cross-Periodogram”

In this section, proofs of lemmas and theorems presented in Section 4.6 on bias and covariance of the frequency-smoothed cross-periodogram are reported.

5.4.1 Proof of Theorem 4.6.3 Expected Value of the Frequency-Smoothed Cross-Periodogram

By taking the expected value of the frequency-smoothed cross-periodogram (4.147) we have

(5.60)

from which (4.150) immediately follows.

In the third equality (4.106) is used. In the second equality, the interchange of expectation and convolution operations is justified by the Fubini and Tonelli Theorem (Champeney 1990, Chapter 3). In fact, defined

(5.61)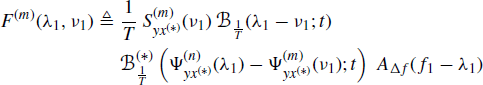

and accounting for Assumptions 4.4.3a, 4.4.5, and 4.6.2, for the integrand function in (5.60) we have

(5.62)

The interchange of sum and integral operations to obtain (4.150) from (5.60) is justified even if the set is not finite by using the dominated convergence theorem (Champeney 1990, Chapter 4). Specifically, by denoting with an increasing sequence of finite subsets of such that , we have

(5.63)

In fact, it results that ...