Growth Curve Modeling: Theory and Applications

7

YIELD–DENSITY CURVES

7.1 INTRODUCTION

Yield–density models describe the functional relationship between the yield of a crop and density of planting. Such relationships are important for determining the optimum plant population level giving maximum yield per unit area.

Two broad forms of yield–density models have traditionally been studied, namely, those classified as either asymptotic or parabolic (Holliday, 1960). Let:

Y = crop yield (dry matter) per unit area

X = density (plant population in number of plants sown per unit area (this notion can also be stated in terms of spatial arrangement))

w = Y/X = mean crop yield per plant¹

If with increasing density Y rises to a maximum and then becomes relatively constant at high densities, then the yield–density relationship is said to be asymptotic (Fig. 7.1a). And if Y attains a maximum and then declines with increasing density, then the yield–density relationship is termed parabolic (Fig. 7.1b). While some yield–density equations involve a relationship between crop yield per unit area (Y) and plant density (X), the vast majority of yield–density models propose a functional relationship between mean yield per plant (w) and density (Fig. 7.1c).

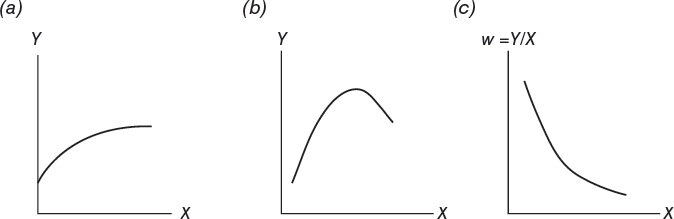
FIGURE 7.1 Yield–density functions: (a) asymptotic; (b) parabolic; and (c) decreasing mean yield.

7.2 STRUCTURING YIELD–DENSITY EQUATIONS

A variety of functional forms for yield–density equations ...