関数型プログラミングの学習

第2章 数学的予備知識

この作品はAIを使って翻訳されている。ご意見、ご感想をお待ちしている：[e-mail]

この章では、あなたが知っておく必要がある（そして過去のある時点で学んだかもしれない）いくつかの点を紹介する。数学的な観点からもコンピュータサイエンスの観点からも、関数に関する基本的な点をほとんどカバーしている。数学的な復習が必要なければ、この章は飛ばして第3章に進んでかまわない。

セット理論

集合論は巨大な分野である。私たちのセットには、集合論の基本的な定義がいくつか必要なだけだ。 あなたは、集合論が集合の定義を提供すると考えるだろう。実際、集合は集合論では未定義の用語として扱われ、我々は非公式にオブジェクトの集合として考えている。偶数の集合、0、1、2からなる集合、母と父を含む集合など、集合として考えられるものはすべて集合である。¹ 私たちは一般に、集合を大文字のA、B、Cなどで表す。集合に含まれるものを要素と呼び出す。Aのすべての要素がBの要素でもある場合、図2-1にあるように、AはBの部分集合である、あるいはAはBに含まれると言う。

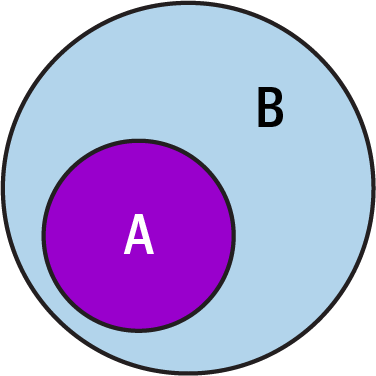
図2-1. AはBの部分集合である

2つのセットの積集合とは、図2-2を見ればわかるように、AとBの両方に存在する 要素をすべて含むセットのことである。

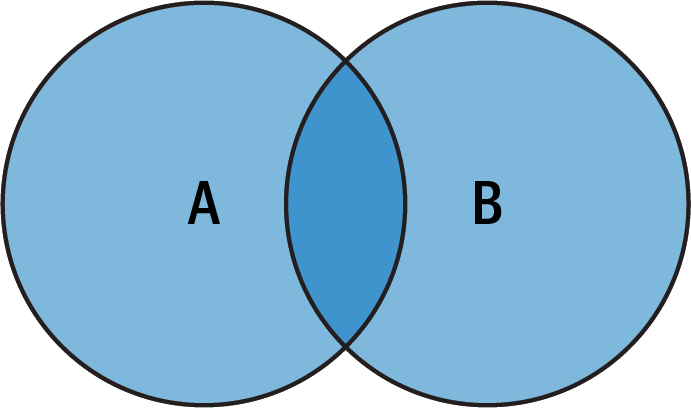
図2-2. AとBの積集合

AとBの和は、AまたはBに含まれるすべての要素 。図2-3を参照のこと。

図2-3. AとBの結合

関数

平たく言えば、関数とは、あるセットの要素を別のセットの要素に関連付ける規則（）である。ここでの考え方は、物事の束があり、その一つひとつをもう一つの物事の束の中の何かと関連付けるということだ。数学の簡単な例として、すべての整数に定義される2乗関数がある。この関数は各整数をその2乗にマッピングする：1は1に、2は4に、3は9に、といった具合だ。また、-1は1に、-2は4に、といった具合だ。このように、関数は2つの異なる値を同じ値に変換することができる。その逆は真ではない。つの要素を2つの異なる要素にマッピングすることはできない。関数が定義されるものはセットである。

領域と範囲

関数は、 要素の束に対して定義される。より数学的な言い方をすれば、要素のセットである。関数が定義されているすべての要素のセットを関数の定義域と呼ぶ。ここで重要なのは、ある関数を定義する式、例えば2乗関数があったとして、正の整数をすべて定義域に選ぶこともできるし、正負の整数をすべて定義域に選ぶこともできるということだ。どちらも2乗関数で定義されているにもかかわらず、これらは2つの異なる関数とみなされる。したがって、関数を定義するときは、必ず定義域を指定しなければならない。

関数の範囲とは、ドメイン内のある要素にマッピングされるすべての要素のセットである。定義域がすべての整数に等しい2乗関数の例では、ある整数の2乗であるすべての整数が範囲となる。この場合、整数の2乗は常に0か正の整数なので、範囲は正の整数すべてとなる。 ...