Chapter 4. Collections
The
single most common type of question encountered on
Sun’s Java Developer Connection forums has to do
with the usage of collection classes in the
java.util package. Since there are many Java
developers out there that have migrated from other professions, this
is not surprising. Those who haven’t taken
university-level data structures courses may find the collections to
be a bit confusing.
However, the proper use of collections is one of the cornerstones of quality Java programming. Therefore, this chapter will explore them in detail. We will cover the architecture of the collections framework and the usage and concepts behind each collection type. However, we won’t cover many of the actual methods in the collections, since these are easily understood by studying the Javadoc. The goal of this discussion is to help you decide which collection to use and why it is the best for a specific job.
Collection Concepts
During the early days of object-oriented programming, one of its main deficiencies was its inability to manage collections of objects. For years, C++ suffered because the collections management that was available was not standardized. To attack this problem, various vendors designed packages of collection classes that could be purchased and implemented. However, even these packages did not solve the portability problem among cooperating vendors. For example, if my company had bought Rogue Wave Tools.h++, all of your business partners would have needed to make a similar purchase to extend your software.
To fix this fundamental deficiency, Sun introduced standard collection classes in the earliest version of the JDK. This decision, along with the other common class libraries in the JDK, contributed to the rapid rise of Java technology. Now, instead of my partner companies having to make a separate and often expensive purchase, they can simply use the collections in the JDK.
An Interface-Based Approach
The JDK collection classes can be found in the
java.util
package. They are
structured using an interface-implementation model. For each type of
collection, there is one interface and various implementations. For
example, the List interface is implemented by the
AbstractList, ArrayList,
LinkedList, and Vector classes.
Tip
Don’t worry about these implementation classes for now; we will discuss them later in the chapter.
Interfaces
are a special approach to object-oriented engineering. While classes
implement the concept, the interface defines the concept. For
example, an ArrayList and a
LinkedList are both conceptually lists.
The interfaces of the java.util package are the
only components that should be exposed to the users of your classes,
unless you have no other choice. This follows from the idea of
encapsulation,
which dictates that the programmer should not expose implementation
details to the user of a class, but only the interface to that class.
For example, the following code is an example of a good
interface-based technique:
public class SomeClass {
HashSet someSet = new HashSet( );
protected Set someMethod( ) {
return this.someSet;
}
}In this example, the programmer exposes only the interface of
someSet to the users and does not let them know
which implementation is being used. Code programmed in this manner is
very flexible and bug-resistant. For example, if you decide that
HashSet does not perform well enough, you can
always change the implementation without affecting the users of the
class. By contrast, consider the following code, which does not use
interfaces:
public class SomeClass {
HashSet someSet = new HashSet( );
protected HashSet someBadMethod( ) {
return this.someSet;
}
}In this example, if you found a bug that occurred because you were
using a HashSet, you could not easily change the
implementation used for the set. If you did, you would then have to
change all of the code that is using your class. This could echo
around your code base for quite a while as you chase bugs.
You should expose the underlying collection implementation in your code only when you have no other choice, such as when the users of your code need access to a specific functionality of the implementation. In fact, this is a good policy to follow within classes as well. The example would have been much better written as:
public class SomeClass {
Set someOtherSet = new HashSet( );
protected Set someOtherMethod( ) {
return this.someOtherSet;
}
}In the revised class, you leverage the usage of interfaces for the
instance variable type and for external communication. This gives you
even more protection from migrating bugs that may result from an
implementation change. If another method in the class uses
someOtherSet as a Set and not a
HashSet, then you can easily change to another
Set implementation as the need arises.
Collection Types
Now that you have mastered the interface approach, you should examine
the actual interfaces in the java.util package and
the differences between them.
There are two types of general collections that form the basis of all collection classes:
-
java.util.Map This interface represents collection types that store values in a lookup table. Each value is stored by using a key that can later fetch that value from the map. Maps can take many forms; one recognizable form is a dictionary. A dictionary class stores words and their definitions. The
java.util.Mapclasses work the same way.-
java.util.Collection This interface represents generic collections other than those that store values in a key-based lookup table. These collections have a variety of access mechanisms.
These two interfaces form the conceptual base for the entire
java.util package. Other collections that extend
the conceptual basis are derived from these interfaces.
Maps
The java.util.Map
class
defines a map that is unsorted and iterated in a fairly unpredictable
manner. In fact, one of the warnings for the
Map
class in the Javadoc is that the
iteration order is not predictable. This is not
a problem in many situations, such as storing event listeners that
listen for specific events. In this case, the key could be the event
type and the value store could be a set of listeners; since the map
would never be iterated in order, having a defined iteration order is
not needed.
However, there may be times when you want more control over the
iteration order of a Map. For example, if you are
creating a tree control to show the files on a
user’s computer, you may want to display these
objects in alphabetical order for easy reading and interaction. For
this purpose, you would need a specialized kind of map:
-
java.util.SortedMap This interface extends a map to specify the iteration order of the keys in the map. This map has a restriction: it can only use keys that it can sort. You must give the class a
Comparator, which is an implementation of thejava.util.Comparatorto implement the sorting, or you must use keys that implement thejava.lang.Comparableinterfaces.
Other than the difference in iteration order, the main difference
between SortedMaps and Maps is
that SortedMaps are generally slower when it comes
to inserting and removing items because the map must rearrange itself
to accommodate new values. Regular Maps
don’t have to worry about these issues. For this
reason, you should use only a SortedMap if you
must have a fixed iteration order.
One thing that Maps and
SortedMaps have in common is that they are unable
to contain the same key more than once. Each key has a defined and
assigned value. If you add a new element to a map with a key that the
map is already using, the map implementation will simply replace the
old value with the new one.
Collections
The
Collection interface
has several variants that are used to extend the
Collection functionality. The
Collection
class itself defines only collections
of objects and says nothing about their iteration order, method of
access, or ability to contain duplicates. However, it is fairly
uncommon for developers to directly use a
Collection to store anything. Usually, you need to
be more specific about the constraints of your
Collection. For this purpose, the JDK provides you
with three types of Collections:
-
java.util.Set Sets are collections that do not guarantee the order in which they will be iterated. However, they do guarantee that no duplicates will be found inside the set.
-
java.util.List Lists are collections that are in a specific order and can be accessed through a numerical index. They can also contain duplicate elements. Note that just because the elements are arrayed in an order doesn’t necessarily mean they are sorted. The elements in a list are usually in the same order in which they were inserted. They may or may not be sorted, depending on the programmer’s needs.
-
java.util.SortedSet Sorted sets maintain the order of the objects within the set, depending on one of two criteria. Either the objects are sorted according to their natural sorting order, as defined by their implementation of
Comparable, or they are sorted using a supplied comparator. We will discuss the specifics of both procedures later in the chapter.
Now that you have all of the nifty features of these subtypes, the
question becomes, “What good is the
Collection interface?” The first
reason it exists is because it provides a conceptual basis for all
collections. The second reason is to give the collections an easy way
to convert from one type of collection to another. In this manner,
you can copy lists to sets, and so on.
Implementations
Now
that you have the various types of collections in mind, it is time to
turn your attention to the implementation of these collections. A
List, for example, can be implemented a number of
ways, each with advantages and disadvantages. However, before you can
understand the various implementations of Lists
and other collections, you need to understand how collections and
maps determine equality and order.
Determining Equality and Order
Until now, we have been
discussing equality and order quite a bit, but without explaining how
these conditions are actually discovered by the collections. For
example, how does a Map decide if two keys are the
same, and how does a SortedSet determine the order
used to sort the objects? To answer these questions, you have to
tackle the basic principles of object equality: identity and
comparability.
Equality versus identity
For many collections to do their job, they need to know which objects
are equal. For example, a Set
can’t exclude duplicate entries if it
doesn’t know how to check to see whether supplied
objects are equal. These collections take advantage of the fact that
all objects in Java descend from the common class
java.lang.Object.
Since all objects descend from Object, the
Set implementations can call the method
equals( )
on all objects. This allows the set to
compare objects. However, there is one catch: for this to be
effective, the object must define (or inherit) a valid implementation
of equals( ).
The default implementation of equals( ) compares
two objects to see whether they are the same object in the virtual
machine by identity
, not by
equality. Suppose you create two
Address objects that define the addresses of
employees. Both address objects can contain the same street name,
number, country, postal code, and other data. However, these objects
are two different instances (and therefore reside at two different
memory addresses). In this case, the Address
objects are equivalent, but they are not the same object—i.e.,
they are not identical. If you use the default implementation of the
equals( ) method, you would always get a result of
false despite the fact that the objects are equal.
To solve this problem, you need to override the definition of
equals( ) to compare the actual data in the class.
While creating your new equals method, you need to
keep the following requirements in mind:
The method must consistently return the same value for any single comparison of objects
xandyno matter how many times the comparison is run, assuming that no data changes inxandy.The method should be symmetric so that
x.equals(y)returns the same result asy.equals(x).The method should be transitive so that if
x.equals(y)andy.equals(z)returnstrue, thenz.equals(x)also returnstrue.Whenever the comparison is against a
nullvalue, the method should always returnfalse—i.e., (x.equals(null) == false)should betruefor all types ofx.The method should be reflexive so that
x.equals(x)is alwaystrue.
Tip
Don’t forget to override the implementation of
hashCode( ) when you override equals(
). There is a contract between these two methods that says
that any objects evaluating as equivalent must also return the same
hash code. For more information on this contract, see the Javadoc for
java.lang.Object.equals( ).
The overridden equals( ) method ensures that
collections that are not supposed to contain duplicates do indeed
prevent them. It also illustrates an important concept in
programming. Two objects are said to be equal in
identity if they are the same object instance,
whereas two objects are said to have equality if
they contain the same data.
Comparing objects
The problem of sorting in collections is solved by defining a way to
compare two objects. This can be accomplished using two different
techniques. The first technique is to have the objects implement
java.lang.Comparable. The
Comparable interface contains a single method
defined by the following signature:
public interface Comparable {
public int compareTo(Object o);
}The compareTo( ) method returns an integer
indicating the comparison of the this object to
the target object. If compareTo( ) returns a
negative integer, then the this object is said to
be less than the object given in the parameter o.
If the returned integer is positive, then the this
object is greater than the given object. If the integer is
0, the object is comparatively the same as the
this object. Generally, implementations will
ignore anything other than whether the return value is positive,
negative, or 0. Therefore, it is useless to worry
about defining how much less than the given object the return value
is. For example, a returned value of -8 would be
treated the same as a returned value of -1.
One important factor to remember about this comparison is that it
does not compare equality. Two objects that are
not equivalent may result in a compareTo( ) result
of 0. This occurs often when objects try to sort
on only one or two fields in the class. For example, if you consider
a Person object, you would want to sort on first
name and last name but not necessarily on the other fields, such as
age and tax identification number. In this case, compareTo(
) would return a value of 0 for two
people named Paul Henry despite the fact that one is a senior
executive and the other is an infant.
The compareTo( ) method has a number of
requirements similar to the equals( ) method:
Like the
equals( )method, thecompareTo( )method must return the same value for any single comparison of objectsxandyno matter how many times the comparison is run, assuming that no data changes inxandy.The method should be transitive—i.e., if object
xis comparatively greater than objecty, and objectyis comparatively greater than objectz, objectxshould be greater than objectz. This is generally written using the following mathematical notation:If x > y and y > z then x > z
The method must ensure that the comparison is consistent. For example, if
x.compareTo(y)yields-1, theny.compareTo(x)should yield1.The method should be reflexive so that
x.compareTo(x)always returns0.It is recommended that objects that are comparatively
0, but are not necessarilyequals( ), indicate this in the documentation to the class.
It is always a good idea to implement the
Comparable interface for objects that may be
stored inside ordered collections. This implementation defines what
is known as the natural
ordering
of instances. However, there are some
situations in which a developer may want to sort the objects in a
collection based on a value other than the natural ordering. The
java.util.Comparator interface is used for this
purpose.
Suppose you have a set of data objects that contain a variety of
information, and you want to be able to sort that information to
achieve something other than the natural ordering. For example, if
you have a set of Person objects, you may want to
sort them by age or occupation instead of name. To accomplish this,
create a new implementation of the Comparator
interface that will sort the objects. Example 4-1
shows a Comparator that sorts
Person objects based on their tax identification
number.
package oreilly.hcj.collections;
import java.util.Comparator;
import oreilly.hcj.bankdata.Person;
public class TaxIdComparator implements Comparator {
public int compare(final Object x, final Object y) {
return ((Person)x).getTaxID( )
.compareTo(((Person)y).getTaxID( ));
}
}In this example, you take advantage of the compareTo(
) method built into java.lang.String to
compare the two people based on the values of their
taxID property. Now that you have a new
Comparator implementation, you can sort the people
by passing this comparator to sorting collections:
public class SomeClass {
protected void demoComparator( ) {
SortedSet people = new TreeSet(new TaxIdComparator( ));
// . . . add people to the set.
}
}Once you have created the sorted set and assigned the comparator, you
can be sure that the people inserted into the set will always be
sorted in order of taxID. You can also implement
more complicated comparators that are configurable.
Big O Notation
Implementing collections in programming languages has been a topic of computer science since the first days of structured languages. This topic was born out of the desire to efficiently store and analyze information in computer systems. It is a true science with theories, mathematics, and concepts. One of the most important pieces of mathematics necessary to understanding collections is the concept of Big O Notation. Big O Notation is a mathematical term used to express the efficiency of an algorithm depending on the number of elements the algorithm must work on. The notation is called Big O Notation because of the conspicuous usage of the letter O in the formulas. The O stands for orders of magnitude . The general idea is that the lower the orders of magnitude, the faster the algorithm is.
Consider a list of people stored in a random order. Big O Notation
will tell you how long, on average, it will take you to find any one
person in the list by name. If you think about the worst-case
scenario, you will realize that you may look through all of the
elements in a list, only to find that your target person is the last
element on the list. As the list grows in size, your worst-case
scenario gets . . . worse. If you have 100 people in your list, your
worst-case scenario would involve performing 99 checks to find a
person. If your list is 100,000 people, then you would have to do
99,999 checks before you find the person. This is described in Big O
Notation with the formula O(n). This shorthand is
read as “the orders of magnitude grows in proportion
to n.”
By contrast, if you store people that are sorted by name in an
ordered list, you can use a binary search algorithm to find the
target person, called x, by name. This algorithm
compares the person at the halfway point in the list,
y, to the target person. If the person
x evaluates as equal to person
y, then the person is found, and the algorithm
stops. However, if the person x evaluates as
greater than person y, then the algorithm uses the
upper half of the list for the search. If person x
evaluates as less than person y, the algorithm
uses the lower half of the list. The algorithm then splits up the
targeted half and repeats the splitting process until it finds the
person or narrows the list to one person that isn’t
the target person.
The binary search algorithm has an order
of magnitude of O(log2(n)). This means that the
worst-case scenario to find a person in a list of size
n is the result of
log
2
(n).
In the case of your 100,000-person list, the result of this equation
is roughly 16.609 operations. In other words, the worst-case scenario
is that you would need 17 compares to find the target person.
Tip
Most calculators have only a
log
10
(n)
function. To find
log
2
(n)
on these calculators, you can employ the simple formula
log
2
(n)
-
log
10
(n)/log
10
(2).
The most common orders of magnitude that you will encounter are the following. They are listed in order of most efficient to least efficient.
-
O(1) Constant time. No matter how big the list, the time to find the target is always the same.
-
O(log2(n)) This notation is often abbreviated
O(log(n)). For 100,000 people, the value would be 17 compares.-
O(n) For 100,000 people, you would need 99,999 compares.
-
O(n×log(n)) For 100,000 people, you would need 1,700,000 compares!
-
O(n2) My computer couldn’t compute this result for 100,000 entries; however, for 100 entries, it is 10,000. This number increases very rapidly.
-
O(n!) The factorial is the series of integers from 1 to
nmultiplied together. For example, ifn=10, the factorial is10×9×8×7×6×5×4×3×2×1=3628800. If you write an algorithm with this order of magnitude, you will definitely have problems.
Big O Notation is not limited to calculating search time in a
collection. In fact, it can be applied to any computer algorithm as a
measure of efficiency. Generally, algorithms higher than
O(n) are not feasible as solutions to practical
problems.
Lists
Now
that you have an understanding of the basic concepts, you are ready
to study various types of collections. Once you have decided that you
need a List, the next step is to decide exactly
which List you need to use. To make a good
decision, you need to have a good understanding of the three standard
implementations of List.
Tip
Although anyone can implement the collection interfaces in their
code, we will stick to the classes defined in the
java.util package. Personally, I like to augment
this with the collections classes from Jakarta Commons, available at
http://jakarta.apache.org/.
java.util.Vector
The Vector
class has been with the JDK for quite a
long time. If you look at the @since tag in the
Javadoc for this class, you will see that it was introduced in JDK
1.0.
A Vector is essentially a
dynamic resizing array. You create a
vector by specifying its initial size and the size of the chunk you
want to use to resize the Vector should it exceed
its storage capacity. The following code creates a
Vector that starts with 100 elements and grows by
100 elements (when needed):
Vector v = new Vector(100, 100);
Tip
There are other constructors to vectors that use default values for
sizes and increments. Additionally, there is an extra constructor for
Vector that copies a collection into a
Vector and uses the default value for
incrementation.
Since Vector is an implementation of the
List interface, instances of
Vector also allow the user to access each element
in a similar manner to that of an array. Therefore, you can think of
Vectors as something of a resizable array.
In fact, inside the Vector class, the data is
stored as an array of objects. When you initialize the
Vector, this array is allocated according to the
initial size that you specify in the constructor. As the
capacity of the Vector is
exceeded, a new array is allocated that is equal to the size of the
old array plus the capacityIncrement you specified
in the constructor. If you didn’t specify either of
these values, the class uses its default sizes.
When the Vector class has to resize, it copies the
old array into the new array using the System.arraycopy(
)
method. Although this method uses fast
native code to copy the array, copying is still quite slow and will
get slower as the size of the Vector grows. This
is why it is important to assign values to
capacity and capacityIncrement
that minimize the number of resize operations without wasting too
much memory.
Using an array to store the data inside a Vector
has one other major disadvantage. When inserting an element into a
Vector at a specific position, the
Vector must use System.arraycopy(
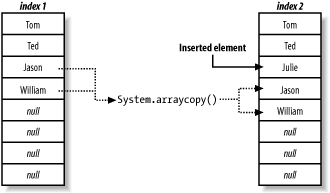
) to move the data to accommodate the insertion, as Figure 4-1 demonstrates.
Figure 4-1 shows the result of inserting a
String element at index 2 into the
Vector. Since there was already an element at
index 2, the Vector had to use
System.arraycopy( ) to push the elements further
down into the array. If you remove elements at an index, the same
process has to be performed to compress the array.
What this all adds up to is that Vector is not
very good at inserts and removals of items. However, the array
storage paradigm makes Vector very good at
accessing elements quickly. Therefore, Vector is a
good choice for a list whose prime function is to access the data in
the list rapidly, and a poor choice if the data in the list will be
modified frequently.
However, the Vector
class has one major problem: since
Vector was designed to be thread-safe, it is
replete with synchronized blocks in the code. This
allows multiple threads to use a Vector safely,
but significantly slows down its performance. The semantics of
synchronized code are outside the scope of this book; however, I can
tell you that the process of synchronization is a costly one.
Tip
If you are interested in learning more about synchronization and thread programming, check out Java Threads by Scott Oaks and Henry Wong (O’Reilly).
In situations in which data structures will not be accessed by
multiple threads or in which the synchronization can be provided
outside of the list, using Vector is a sad waste
of performance. However, if you will be tossing your list around
various threads, you should stick with Vector.
java.util.ArrayList
The ArrayList
class is JDK 1.2’s
answer to the synchronization problem in the
Vector class. This class does essentially the same
job as the Vector class but without
synchronization. The lack of thread safety within the
ArrayList class makes it much faster than
Vector. However, it still suffers from the same
performance problems as Vector when resizing,
adding, or removing elements.
If you need a class that has all of the features of
Vector but not the internal synchronization, you
should choose a list class.
java.util.LinkedList
The LinkedList
class also implements the
List interface and allows you to store objects in
a defined order. However, it implements this ability in a very
different way than Vector or
ArrayList.
Whereas Vector and ArrayList
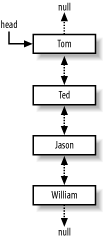
hold their data in an array of objects, LinkedList
uses a special node structure to connect the objects. Each object is
stored in a node that contains three attributes: one to contain the
data in the node, one to be used as a reference to the next node, and
one to be used as a reference to the previous node. The start of the
chain of references is usually referred to as the
head of the list, and is the only node actually
stored in the class variable. The structure of a
LinkedList is shown in Figure 4-2.
This node-based structure makes it easy to insert or remove elements
in the LinkedList. All that the list needs to do
is create a node and rewire the references to the previous and next
objects. There is (thankfully) no need to copy references or perform
any other costly actions.
On the other hand, the structure of a LinkedList
makes finding any particular element in the list a costly exercise.
Since the LinkedList class has to step through the
nodes one by one from the head of the list until the element is
found, the search will be slow.
Tip
Some of the data structure purists out there may have noticed that
LinkedList is, in fact, not a normal linked list
at all. In fact, a normal linked list has only a reference to the
next object and not a reference to the previous object. The
LinkedList class in the
java.util package is actually a doubly
linked list.
For these reasons, LinkedList is a great class for
manipulating data and shuffling it around. It is ideal for tasks such
as sorting and performing frequent insertions and removals. However,
it is really bad at accessing data quickly. You should use
LinkedList if the primary function of your list is
to manipulate data in the list.
Maps and SortedMaps
Maps
are useful structures for storing things such as key/value pairs. The
Map interface and its descendant
SortedMap have many implementations. Once you have
decided that you need to use a map as your collection, you will then
need to decide exactly which map to use.
java.util.HashTable
The Hashtable
class is one of the two grandfathers of
Java collections, the other being Vector. The
Hashtable class stores a series of keyed values in
a structure that uses the hash code of the object to store things
quickly. To understand how a Hashtable works, it
is important that you understand the hash system.
When a Hashtable is constructed, it creates a
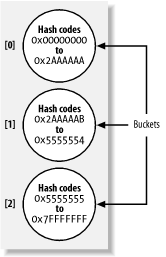
table to hold the data of the collection. This table is an array of
arrays. Each of the subarrays represents a bucket in which the class
can store a set of values. All of the buckets are the same size.
As you insert new items into the table, the hash code of the object is used to determine which bucket the object should go into. Once the correct bucket is found, the object is inserted into that bucket. The structure of the class is shown in Figure 4-3.
Each bucket holds data within a particular range of hash codes. As you add items to the table, the hash code of the key is computed and the correct bucket is chosen.
One of the advantages of this structure is that it can hold very
large data sets without impeding performance. As the map grows, the
number of buckets grows, and the range of hash codes allowed in each
bucket gets smaller. The result is that the map can find any object,
taking, on average, the same amount of time as it does to find any
other object. In Big O Notation, this is referred to as
O(1). This is the best-case scenario for algorithm
efficiency.
As the map grows, it fills up until its load reaches a certain
percentage. This loadFactor can be given to the
class at construction time, or the user can choose to use the default
value of 0.75f. When using the default, as soon as
the map becomes 75% full, the class will increase the size of the
map, usually by creating more buckets and narrowing the range. Once
the new map is ready, the class will rehash the
map by computing the hash codes of each object in the map and filing
them in their proper buckets. This is a fairly slow process, so you
don’t want to do it often. On the other hand, since
hash-based data structures take up a lot of memory, you
wouldn’t want to allocate maps with huge initial
capacities either. Finding the optimal performance for a hash-based
data structure is often dependent on how the class will be used in
the program. If the data size in the map is fairly constant, you can
use higher load factors. However, if the data is constantly changing
size and memory is tight, you may want to use lower load factors. The
default size of 0.75 provides this good balance in
most situations.
The Hashtable class is indeed useful. However, it
is internally synchronized, which makes it thread-safe but much
slower than other alternatives.
java.util.HashMap
Essentially, a HashMap
is an implementation of the
Hashtable class without internal synchronization.
It sacrifices thread safety for higher performance. Other than this
difference, they are conceptually the same. If you
don’t need to pass your map around in a threaded
environment, or if thread safety can be provided externally to the
map, then you should use a HashMap.
java.util.LinkedHashMap
A LinkedHashMap
is an implementation of the
SortedMap interface that allows you to guarantee
that the iteration of the keys is in a predictable order. It uses the
same technique as the HashMap and
HashTable classes to store the data. However,
LinkedHashMap also maintains a running
LinkedList that contains all of the keys in the
map in a sorted order.
Although keeping the keys in a sorted order is advantageous when it
comes to iterating through the map, maintaining the extra linked list
causes LinkedHashMap to be slower than
HashMap. Use it with caution.
java.util.IdentityHashMap
An IdentityHashMap
is the same as a
HashMap, except that objects are compared based on
identity, not equality.
In this map, key objects evaluate as equal only if they are the same
instance in the virtual machine. This differs from other collections
that evaluate for equality based on the result of calling the
equals( ) method.
Since this map doesn’t compare based on equality,
you can insert multiple keys into the map even when they evaluate as
equals according to the equals( ) method; they
only need to be different instances. For example, the following two
instances could be placed in the same
IdentityhashMap:
String x = new String("tom");
String y = new String("tom"); // <== Different instance!
IdentityHashMap ihm = new IdentityHashMap( );
ihm.put(x, new Integer(15));
ihm.put(y, new Integer(8));If you try this with a normal HashMap, the value
for the key tom would be replaced on the second
line. With an IdentityHashMap, both values are
inserted. However, just because you can do this
doesn’t mean you should; I don’t
recommend inserting duplicate keys into an
IdentityHashMap because it can result in some very
confusing code.
All other operations on an IdentityHashMap work
the same way as they do on a HashMap. The
following code takes up where the last snippet left off:
String z = new String("tom");
Integer obj = ihm.get(z);In this code, the variable element will contain the value
null. This is because z is not
the same instance as x or y
even though they contain the same value. When working with
IdentityHashMaps, you should keep these gotchas in
mind.
java.util.WeakHashMap
A WeakHashMap
is just like a
HashMap, except that the keys used in the map are
stored in weak references. We will cover weak references in Chapter 10.
java.util.TreeMap
A TreeMap
is the other implementation of the
SortedSet interface. However, unlike
LinkedHashMap, the TreeMap
class doesn’t store its elements in a hash-based
data structure. Instead, it stores its elements, unsurprisingly, in a
tree.
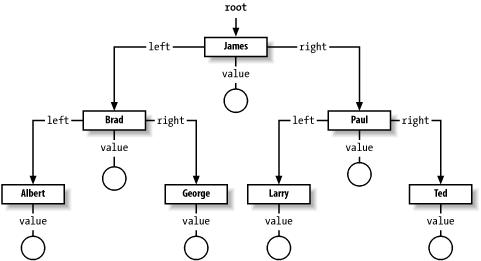
Specifically, the TreeMap class uses a structure
called a binary tree. Figure 4-4 shows how this
structure looks in memory.
Inside TreeMap is a variable called
root, which stores the root of the tree. Each node
in the tree stores a key and a value, and each element stores a left
and a right element. When a new element is inserted, the key is
evaluated against the root. If the key is the same, then the
root value in the root entry will be replaced with
the new value. However, if the key evaluates as less than the
root (compareTo( ) returns
-1), the TreeMap will use the
left member of the root to navigate to the next
element. If the key evaluates as greater than the
root (compareTo( ) returns
1), the TreeMap will use the
right member to navigate to the next element. This
process of evaluation continues until the key is found or the
TreeMap hits a leaf node, which is a node without
a left or right member. If the TreeMap hits a leaf
node, it will add a new entry containing the key and value and tack
it on to the leaf node.
Keep in mind that determining whether a node is a leaf is dependent
on which side, left or right,
to which the TreeMap wants to surf. A particular
node could be a leaf node with respect to left but
not to right, as right may have
a reference to another entry.
Every now and then, the tree will become lopsided—that is, it
has more elements on one side of root than on the
other. When this occurs, the tree is rebalanced by using the middle
key in the sorted keys as the new root entry. The
other entries are then copied into the new tree using the algorithm
for adding new entries. This rebalancing process is slow.
The process of adding or removing a key from a
TreeMap has a O(log2(n))
efficiency. It isn’t as good as a
LinkedHashMap with its O(1)
efficiency, but a LinkedHashMap has to store two
data structures for the elements in the map—one to accomplish
the actual storage and another to keep a list of the keys in a sorted
order. For this reason, TreeMaps are better at
storing large sets of data. Since log2(n) grows
very slowly as n increases, this size trade-off is
often worth the cost.
If you are morbidly curious, where n is
100,000,000, log2(n) is only 26.5754247590989.
This means that if you have a map that contains a hundred million
entries, a TreeMap will be able to find any
arbitrary key using a maximum of 27 compares. That is usually good
enough in most situations. On the other hand, storing references to
all 100,000,000 entries twice would take up too
much memory.
Sets and SortedSets
If you have opted to use a set as your collection, you will first need to decide whether the data needs to maintain a sorting order. This question is more complex than it appears.
For example, a set of contacts in an address book doesn’t necessarily need to maintain sorting order even though the items may be displayed in a sorted order in the interface. In fact, the sorting order may be invalid if you built the list to sort based on last name, and the user wants it sorted based on email address. However, a set that holds the instructions to make a certain part in a factory must be kept in a specific sorted order to ensure that they are followed correctly.
The question you
should ask yourself is, “Do my objects need to be in
a sorted order for presentation only, or is there some other
underlying logical reason for the sorting?” If they
only need to be presented in sorted order, then
you can easily copy them to a list or SortedSet in
the GUI and sort them at presentation time. However, if there is
another underlying logical reason to sort them in one predefined
order, then you should opt for a SortedSet. Try to
avoid sorting your sets. Sorting sets introduces significant overhead
in the insertion and deletion of items in a set and can impede
performance.
java.util.HashSet
A HashSet
is an implementation of the
Set interface that stores its contents using a
hash system. This system works the same way as a
HashMap. In fact, one interesting piece of Java
trivia is that the HashSet class is implemented
using only the key set of the HashMap class. The
HashSet class merely inserts a dummy value for
each key in the map and hides the fact that it is using a map from
the user.
java.util.LinkedSet
A LinkedSet
is an implementation of the
Set interface that guarantees a predictable
iteration order. It does this by maintaining a
LinkedList of the objects in the set, which can
significantly decrease the amount of memory.
Note that just because the order is predictable does not mean that
the order is sorted. In fact, the only real benefit of a
LinkedHashSet over a regular
HashSet is that the iteration of the set remains
constant over time and isn’t as random as
HashSet. However, I have never seen a programming
situation in which this is enough of a concern to balance the
significantly larger memory consumption.
Choosing a Collection Type
When faced with such a wide variety of collections, it is often difficult to decide which collection type you should use. The general rule is that you should use the collection type that is the most restrictive and still accomplishes your needs. The reason for this is that collections tend to slow down as their abilities increase.
First, you should decide whether you need values that can be looked
up by a key. If so, then you are restricted to a
Map type. If not, then you can use a more general
Collection type. If you decide to use a
Collection type, the next thing you need to ask is
whether you need duplicates in your collection. If so, then you will
need to use a List; otherwise, a
Set should suffice.
After you have made these decisions, you should decide whether you
need the objects to be sorted. This decision is much hazier than the
other decisions. Almost all collections will need to be sorted at one
time or another by a user. However, there are other ways of doing
this sorting, such as copying the collection and sorting it in a
list. You should opt for SortedSets or
SortedMaps only if there is a reason why the
collection should always be sorted in a specific manner. Sorted
collections and maps must maintain the sorting order, so they tend to
be significantly slower than other collections and take up more
memory. You should incur this performance hit only if you need the
functionality.
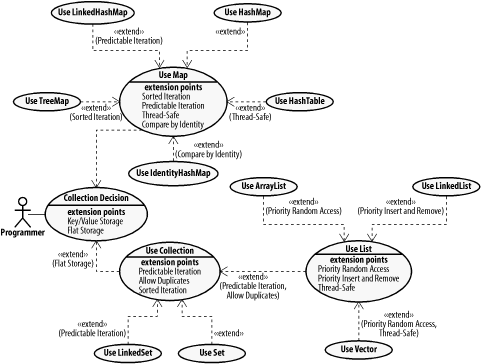
As for choosing the implementations, you need to consider the merits of each type of implementation before determining which is the best. Figure 4-5 should help you make that decision.
In this book, we deal only with the JDK standard collection types. However, the Apache Jakarta Commons project has a library of other collection types that broadens the selection scope significantly. I highly encourage developers to seek out this project at http://jakarta.apache.org/commons/collections.html and take a look at other options.
Iterating Collections
Now that you have the fundamentals of collections firmly in mind, you need a way to iterate through collections. You can accomplish this using three types of iterator interfaces.
The java.util.Enumeration,
java.util.Iterator, and
java.util.ListIterator interfaces are used to
iterate through data objects in a collection. The collections
themselves are responsible for implementing these interfaces and for
providing the iterator for the caller. They do this using inner
classes.
Three Iterators
In the JDK, there are three principle types of iterators. Understanding each of them will help you pick the best one for your particular programming task.
java.util.Enumeration
This is the oldest of the iterators. It
allows you to iterate one way through a collection. Once you pass an
element, you cannot go back to that element without getting a new
enumeration. One problem with enumeration is that it has been
replaced by the Iterator interface. The
Collection and Map interfaces
require the developer to implement an Iterator but
not an Enumeration. Therefore, you probably
won’t use this interface often unless the collection
classes are not available (for instance, during J2ME programming on
some limited profiles).
java.util.Iterator
This interface is the replacement in the
JDK 1.2+ collection class architecture. Not only does it provide the
same functionality as an Enumeration, but it
allows you to remove an element from the collection by calling
Iterator.remove( ). However, using
Iterator.remove( ) can cause some rather confusing
code.
Fail-Fast Iterators
Many collections provide a fail-fast iterator . Essentially, this means that the iterator is designed to fail if the user modifies the list during iteration. For example, consider the following code:
package oreilly.hcj.collections;
public class SomeClass {
protected void markPreferredCustomer(final String someCustomer) {
Set set = new HashSet( );
// . . . add items to the set.
String element = null;
Iterator iter = set.iterator( );
while (iter.hasNext( )) {
element = (String) iter.next( );
// . . . perform some logic
if (element.equals(someCustomer)) {
set.add(new String("p->" + element));
set.remove(element);
}
}
}
}With the emphasized lines, the developer tries to modify the set
while the iteration is still ongoing. The result of such an attempt
will be a ConcurrentModificationException. When
you are iterating through a collection, you must use the iterator
methods to manipulate the list. Also, the Iterator
class allows you only to remove an item. This makes sense because
iterators can iterate over many kinds of collections that often have
different semantics for adding new elements.
In the end, you are better off not using Iterator.remove(
). Instead, you should save the changes you want to make
and execute them after iterating through the collection. Also, if
your collection can be accessed by multiple threads, you should
surround the whole process with a synchronized
block to prevent one thread from attempting modifications while
another is iterating.
Collection Gotchas
Collections provide you with a powerful tool for storing and traversing data. However, they have their share of gotchas that the savvy developer needs to beware of.
Storage by Reference
One of the most prevalent gotchas has to do with how collections store data. Collections store data by making references to that data, not by copying the actual data. This is important to remember because the collection holding the data is not necessarily the only object that can access the underlying value of that data. Since the variables for all constructed types in Java are references, and these reverences are passed by value, another part of your program could have a reference to a data object in your collection.
Failure to Override hashCode( )
When placing collections in a hash-based data set, the collections
will place objects with similar hash codes in the same bucket. This
can be a problem if you forget to override the hashCode(
)
method in your
collected objects.
If you don’t override hashCode(
), the collections will use the default implementation in
the java.lang.Object class. This implementation
needs the memory location of the object to compute the hash code.
However, if you create a lot of objects, it is likely that they will
be close to each other within the memory. The result would be a
HashMap with most of the objects in the first
bucket and few, if any, in the other buckets. Such an unbalanced
HashMap would behave poorly; in extreme
conditions, it could degrade from O(1) to
O(n) efficiency.
The solution to this problem is to make sure you override the
hashCode( ) method to give your data an even
distribution inside the buckets of the hash-based collection. Instead
of calculating based on location, you should calculate based on the
data in the object. However, don’t forget to
override equals( ) if you override
hashCode( ).
Tip
The Jakarta Commons Lang library contains utilities that make creating high-quality hash codes easy. I highly recommend you check it out at http://jakarta.apache.org/.
Lack of Type Safety
One of the most persistent
problems with the Java collection classes is the lack of type safety.
Since the collection classes store Object
instances, a user can insert anything into a collection. This could
easily lead to multiple ClassCastException
instances being thrown. It also introduces problems with quality data
validation, which we will discuss in Chapter 6.
In JDK 1.5, Sun plans to introduce the concept of parameterized types, which will provide this type safety. However, the subject of parameterized types is far outside the scope of this chapter; we will cover them in Chapter 12.
However, until JDK 1.5 hits the market, you need to realize that just because you think the collection contains only one type doesn’t necessarily mean there isn’t a rogue object in the collection. The only solution to this quandary is vigilance and good code management through exhaustive testing and checking.
Collecting Problems
There are many things that you can do with Java collections. However, like any power tool, you can do a great deal of harm if you aren’t careful. See Example 4-2.
package oreilly.hcj.review;
public class Customer extends Object implements Serializable {
private Set purchases;
public void setPurchases(final Set purchases)
throws PropertyVetoException {
final Set oldPurchases = this.purchases;
vetoableChangeSupport.fireVetoableChange("purchases", oldPurchases,
this.purchases);
this.purchases = purchases;
propertyChangeSupport.firePropertyChange("purchases", oldPurchases,
this.purchases);
}
public Set getPurchases( ) {
return this.purchases;
}
}This is almost exactly how my IDE generated my bean property. The
only thing I did was add the keyword final to the
parameter declaration and to the oldPurchases
variable. The class looks pretty good, but it has a huge, gaping
hole.
The getter returns a reference to the Set when
someone asks for it. The problem with returning this reference is
shown in the usage of your property:
package oreilly.hcj.review;
public class BeanCollections {
public static void someFunction(final Customer customer) {
if (customer == null) {
throw new NullPointerException( );
}
Set purchs = customer.getPurchases( );
Set names = new HashSet( ); // going to use to store customer names.
names.add(new String("Jason"));
purchs.add(new String("Fred")); // typo; he meant names, not purchs.
}
}In the above code, a String was added to a
Set that isn’t meant to contain
String objects. After this code runs, a
String object will be inside the purchases
Set that is meant to contain only
Purchase objects. Since adding the
String to the purchases Set
bypasses the setter, the internals of the Customer
object were changed while all type-checking code was being bypassed!
The defective Set is not detected, and the code
compiles, deploys, and still doesn’t break. Down the
line, more code is written for your system:
public void makeCustomerReport( ) {
Set purchases = someObject.getCustomer(12345).getPurchases( );
for (Iterator iter = purchases.iterator( );; iter.hasNext( );) {
Purchase purchase = (Purchase)iter.next( ); // ClassCastException
reportingObject.add(purchase);
}
}Because there is a String object in a
Set that is supposed to contain only
Purchase objects, a
ClassCastException is in this piece of code. This
is one of those mysterious bugs that can baffle you for two hours and
then make you want to break something when you figure it out. Worse,
if this bug occurs only intermittently, you have an evil problem to
deal with. However, you can prevent this headache before it even
starts:
package oreilly.hcj.review;
public class Customer extends Object implements Serializable {
public void setPurchases2(final Set purchases2)
throws PropertyVetoException {
final Set newPurchases2;
if (purchases2 != null) {
newPurchases2 = Collections.unmodifiableSet(purchases2);
} else {
newPurchases2 = null;
}
final Set oldpurchases2 = this.getPurchases2( );
vetoableChangeSupport.fireVetoableChange("purchases2", oldpurchases2,
newPurchases2);
this.purchases2 = new HashSet(purchases2);
propertyChangeSupport.firePropertyChange("purchases2", oldpurchases2,
getPurchases2( ));
}
public Set getPurchases2( ) {
if (this.purchases2 == null) {
return null;
}
return Collections.unmodifiableSet(this.purchases2);
}
}The new version of the Customer class can
encapsulate much more efficiently. When setting the purchases
property, instead of copying the reference, you actually copy the
Set itself. When getting the purchases property,
you give the caller an unmodifiable set. The end result is a minor
performance hit but superior code from a debugging and maintenance
perspective. With this technique, if the user tries to add a
String object to the returned
Set, he will get an
UnsupportedOperationException at the line where he
tries to add the String object:
purchs.add(new String("Fred")); // <= UnsupportedOperationExceptionThis prevents the user of the Customer class from
changing the internals of the Customer object
without going through the setter. More importantly, no one can bypass
the property veto listeners and checking code in the
Customer class. You have traded a few clock cycles
for several man-hours. If this technique adopted as a general policy
in your office, the savings could be measured in thousands of
man-hours.
One of the ugly aspects of the setPurchases2( )
method is all of the checks have to account for
null sets. Every time you call the getter of the
purchases property, you have to check for null.
These checks can become a real hassle and make the code difficult to
read. However, with a coding standard, you can avoid all of this
unpleasantness. Example 4-3 shows the optimal code
for your Customer class.
package oreilly.hcj.review;
public class Customer extends Object implements Serializable {
private Set purchases3 = new HashSet( );
public void setPurchases3(final Set purchases3)
throws PropertyVetoException {
if (purchases3 == null) {
throw new NullPointerException( );
}
final Set oldPurchases3 = this.getPurchases3( );
final Set newPurchases3 = Collections.unmodifiableSet(purchases3);
vetoableChangeSupport.fireVetoableChange("purchases3", oldPurchases3,
newPurchases3);
this.purchases3 = new HashSet(purchases3);
propertyChangeSupport.firePropertyChange("purchases3", oldPurchases3,
getPurchases3( ));
}
public Set getPurchases3( ) {
return Collections.unmodifiableSet(this.purchases3);
}
}In the optimal version of your Customer class, the
property purchases3 can never be
null. You have implemented a coding standard in
which the property will always be a Set. It can be
an empty Set if there are no purchases for a
particular customer, but it will always be an initialized object.
This makes your life a lot easier and your code much cleaner. To
illustrate, see Example 4-4, which operates on a
data model that allows nulls in
Sets.
package oreilly.hcj.review;
public static void makeGroupReport(final Set customers) {
if (customers == null) {
throw new NullPointerException( );
}
Iterator purchaseIter = null;
Iterator customerIter = null;
Set purchases = null;
Customer customer = null;
Purchase purch = null;
customerIter = customers.iterator( );
while (customerIter.hasNext( )) {
customer = (Customer)customerIter.next( );
System.out.println("Purchases for " + customer.getName( ));
purchases = customer.getPurchases3( );
if (purchases != null) {
purchaseIter = purchases.iterator( );
while (purchaseIter.hasNext( )) {
purch = (Purchase)purchaseIter.next( );
System.out.println(purch.getItemName( ) + "\t" + purch.getPrice( ));
}
}
System.out.print("Total Purchases = ");
if (purchases != null) {
System.out.println(purchases.size( ));
} else {
System.out.println(0);
}
System.out.println( );
}
}The emphasized lines show the number of checks for
null you have to make. Let’s
compare this to the code in Example 4-5, which does
the same job with a data model that does not allow sets to be
null.
package oreilly.hcj.review;
public static void makeGroupReportBetter(final Set customers) {
if (customers == null) {
throw new NullPointerException( );
}
Iterator purchaseIter = null;
Iterator customerIter = null;
Set purchases = null;
Customer customer = null;
Purchase purch = null;
customerIter = customers.iterator( );
while (customerIter.hasNext( )) {
customer = (Customer)customerIter.next( );
System.out.println("Purchases for " + customer.getName( ));
purchases = customer.getPurchases3( );
purchaseIter = purchases.iterator( );
while (purchaseIter.hasNext( )) {
purch = (Purchase)purchaseIter.next( );
System.out.println(purch.getItemName( ) + "\t" + purch.getPrice( ));
}
System.out.println("Total Purchases = " + purchases.size( ));
System.out.println( );
}
}This code is much cleaner and shorter. Since you never have to test
for null, you can simply grab an
Iterator directly. If a customer has no purchases,
the inner while loop will merely exit when the
call to purchaseIter.hasNext( ) returns
false. Example 4-5 is far
superior to Example 4-4 in terms of code
maintenance, readability, and speed.
The benefits of non-null sets also extend to other
data structures. Collections, maps, and arrays should never be
null, but they should be empty if they
don’t have data.
Get Hardcore Java now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.