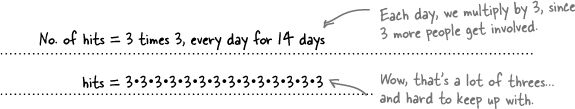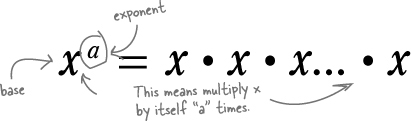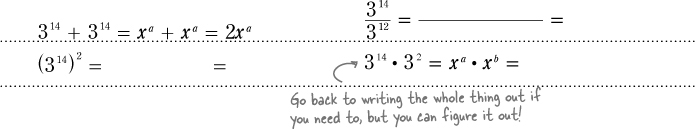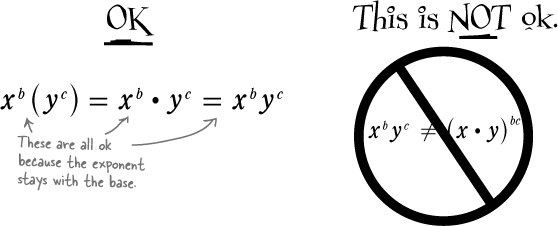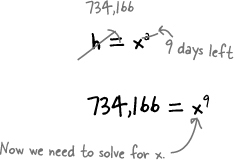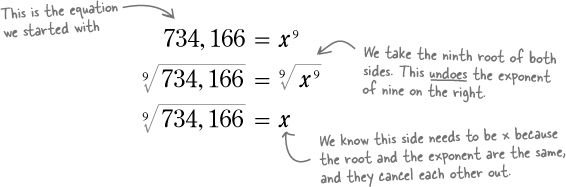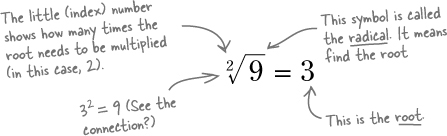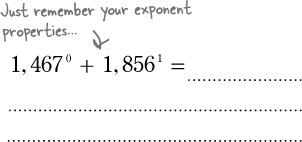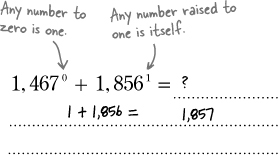Chapter 4. Exponent Operations: Podcasts that spread like the plague (that’s a good thing...)
Could you multiply that again? Could you multiply that again?
There’s another way to express multiplication that’s repeated over and over and over again, without just repeating yourself. Exponents are a way of repeating multiplication. But there’s more to exponents, including some smaller-than-usual numbers (and we don’t just mean fractions). In this chapter, you’ll brush up on bases, roots, and radicals, all without getting arrested for any sit-in protests. And, as usual, zero and one come with their own problems... so jump into a podcasting exponentiation extravaganza.
Addie’s got a podcast
Addie podcasts about crazy celebrities.
Addie’s been getting a lot more listeners lately. To take it to the next level, she needs new equipment to deliver an even better podcast... but that takes a lot of cash.
Addie’s got a website to host her podcasts, and she wants to advertise on her site to raise funds for new gear. She’s lined up some possible sponsors, but they won’t help out until Addie proves she can get some real traffic on her site. Addie needs to:
...monitor the daily hits on her website over the next 2 weeks.
...prove her site can generate at least 5,000,000 hits in the next 2 weeks!
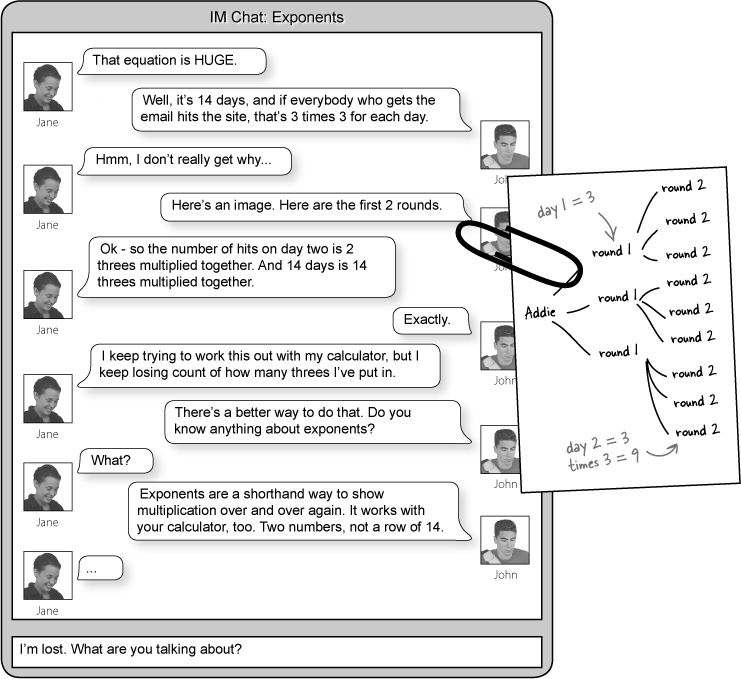
Let’s mobilize Addie’s listeners
Addie knows she’s got big fans. Here’s a letter she’s worked up to send out to her 3 top listeners:
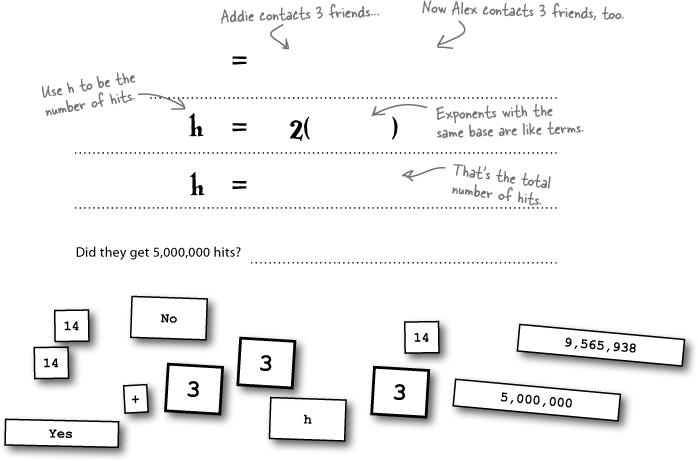
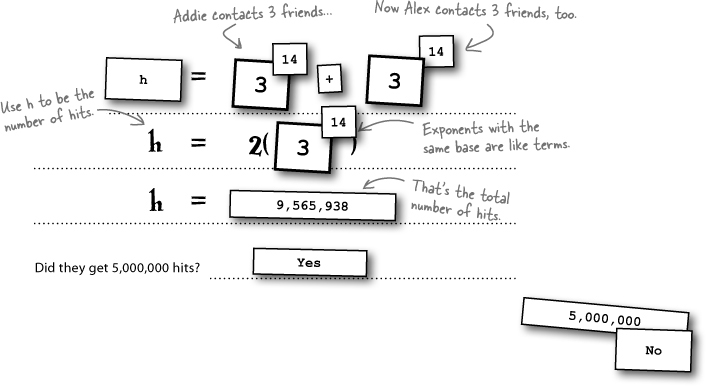
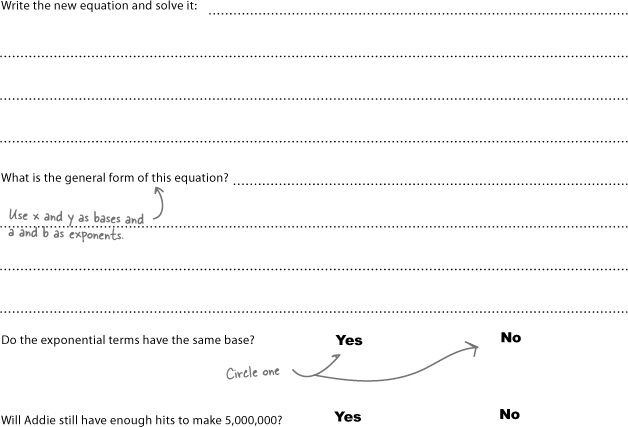
Can Addie and Alex get enough hits?
Alex has offered to send off another round of emails for Addie. He’ll start with 3 friends, just like she did, and try to help get 5,000,000 hits in 14 days.
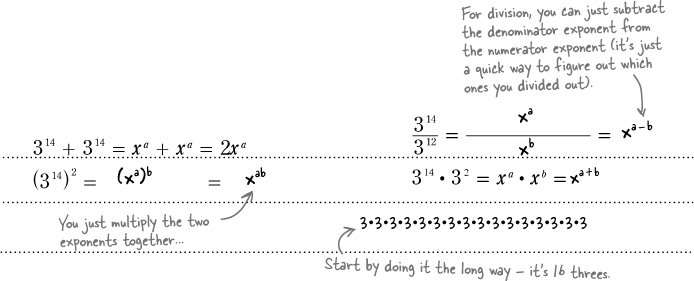
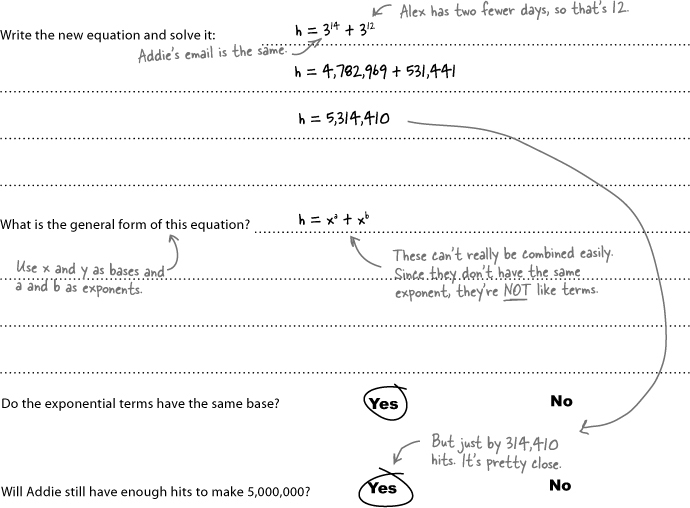
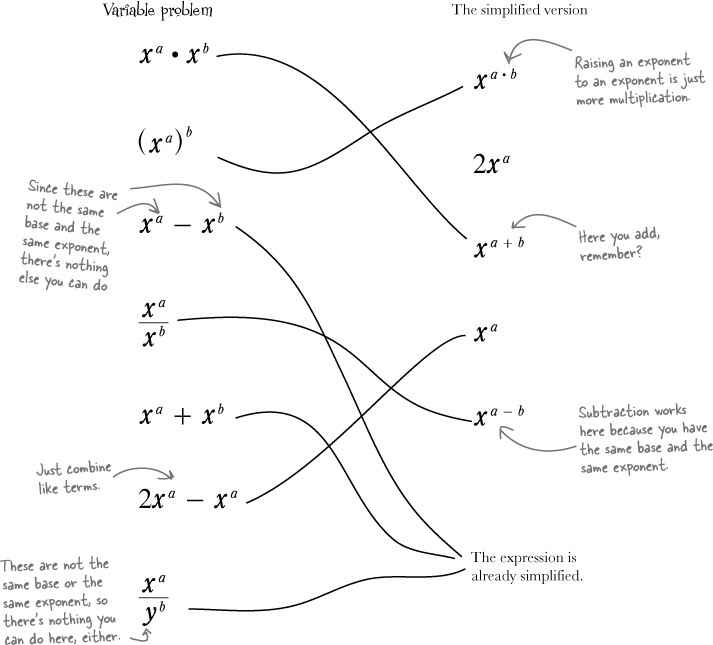
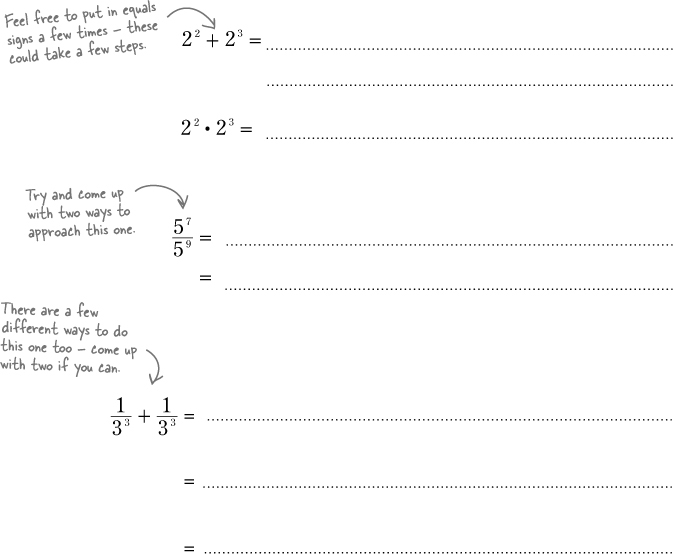
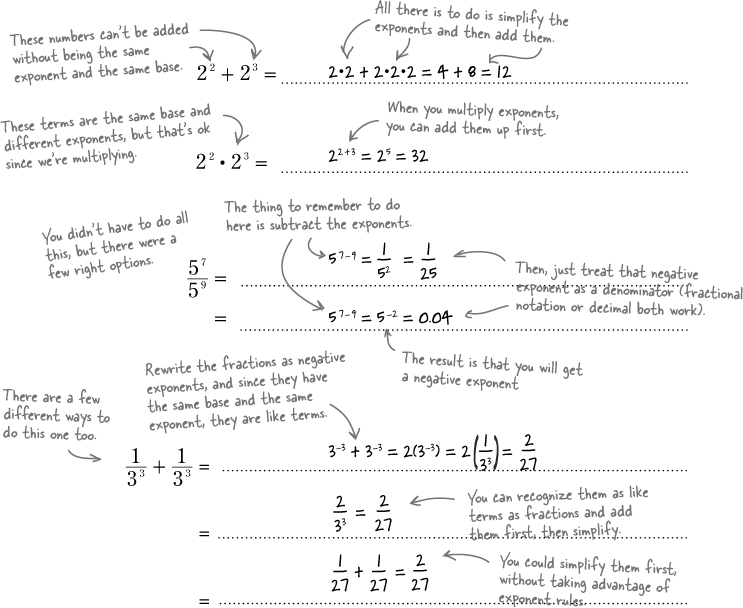
To figure out the total number of hits, you’ll need to figure out how to add up both groups that Addie’s working with. In Chapter 2, you combined like terms to help Paul on his road trip, and this is the same idea. You may remember from Chapter 2 that a term is any part of an equation held together with multiplication or division. Since an exponent is just a shorthand version of multiplication, that means exponential terms with the same base and the same exponent are like terms.
With exponents, you can combine terms that have the same base. Let’s try that out and see how it works:
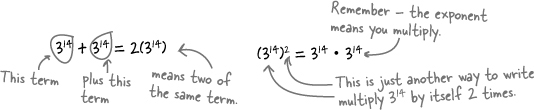
Because (314)2 is multiplication, not addition.
A term is something held together by multiplication, which means that the entire exponential term is treated as a group.
When you group two like terms together, you’re adding those terms together. But if you take those two terms and use exponents (that 2 at the end of (314)2), then you’re multiplying, and that’s not what we want. Look:
Well, that would work, but that’s a lot of threes...
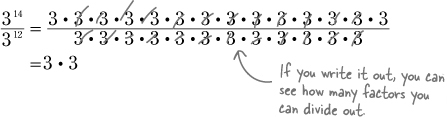
Writing out the multiplication by hand will work; it’s just not very convenient. Look how long this thing turns out to be:
But look, there’s a pattern! Here’s what this means:
Exponents with the same base are LIKE TERMS.
That means they can be added, subtracted, multiplied, and divided.
Try division:
Alex is flaking out on his sister
Alex didn’t send out any emails to his friends until the third day. That means he only has 12 days to get the word out. Will Addie still make it?
There’s always a villain...
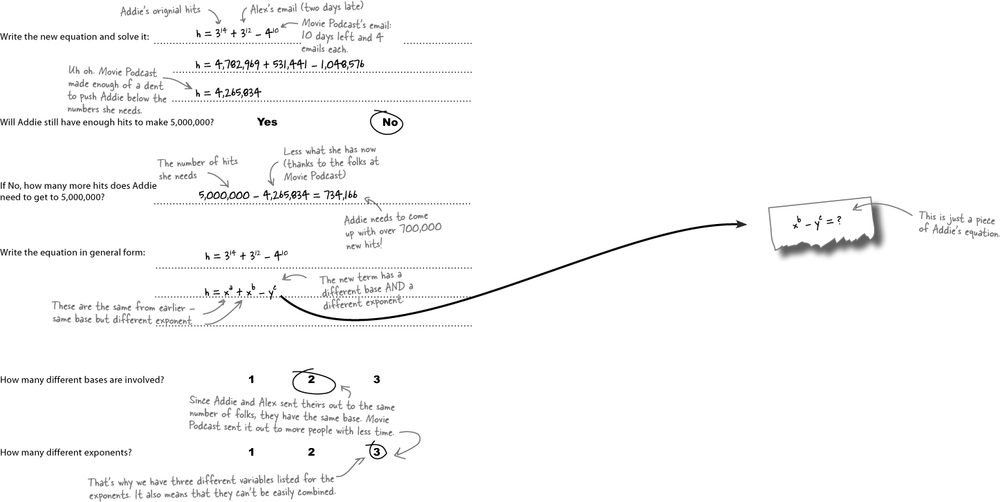
The Movie Podcast heard about Addie’s plan to increase subsribers, and they don’t like it. The sponsorship Addie’s trying to get... well, it’s money out of the Movie Podcast’s pocket. So now they’re fighting back.
Every person that hits Movie Podcast’s page instead of Startalk Podcast’s page is taking away potential hits. What does this mean for Addie’s chances to score a new sponsorship deal?
Different bases = NOT like terms.
Terms with different bases are not like terms (regardless of the exponent). They just don’t have anything in common. As exponential terms, they’re not multiplying the same number, regardless of how many times.
You can’t add exponents with different bases
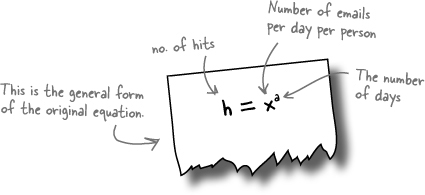
If we just talk about the bit of Addie’s equation that has two terms, it looks like this:
You know that you can’t add or subtract these two because they’re not like terms. Multiplication and division don’t work either. Exponential terms being multiplied together just get written together, like this:
The order of operations says exponents FIRST
You can’t split up bases and combine different exponents because each base has to stay with its own exponent. The order of operations says that exponents go before multiplication. That means the exponents have to be simplified before they can be combined with something else.
Brain Power
Test it out with real numbers - try 32 and 43. Can you show that (32)(43) is not the same as ((3)(4))(2)(3) without working things all the way out to the answer?
Addie needs another round of emails.
But how many does she need to send out? Addie has only 9 days left and she needs to figure out how many emails she needs to start with today to make up for the campaign that Movie Podcast’s running.
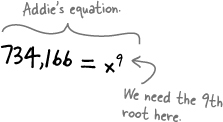
A root is the INVERSE of an exponent
We need an operation that can unravel an exponent. So when we have the exponent, what’s the base to get a certain answer? Well, that’s the root. When you find a root of something, you’re finding the number that can be multiplied over and over to reach the final number.
For Addie, we need take the ninth root of both sides of her equation. That will isolate x and give us a numeric value on the other side.
9 days later...
You’ve helped Addie land a big check!
Addie’s site cleared 5,000,000 hits, no problem. Her sponsorship deals on, the subscribers are pouring in, and Addie’s off to get some great new gear from her local Apple store. Next up... a video campaign on YouTube!
Get Head First Algebra now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.